Egison Blog

Egison Presentation for Rakuten Technology Conference 2017

Oct 31, 2017

In RTC 2017, I made a presentation on Egison. The following are slides and script for that.

#1

Hello, everybody! Thank you for coming my session.

Today, let me introduce my programming language Egison by showing its features that are useful for describing calculations in Riemannian Geometry.

#2

Egison is a programming language that I created. I have been developing it since 2011. I am implementing it in Haskell.

#3

The aim of the development of Egison is to create a language that can directly represent all algorithms that can be discovered and it’s a very big goal. Currently, my biggest challenge is to improve Egison in order to directly represent calculations that appear in mathematical physics.

This challenge is important for computer science because this research will help us to use more advanced mathematics. Mathematics used to solve the problems in Computer Science depends on mathematics that we can describe easily by programming languages. So extending the area of mathematics we can describe is very important.

#4

The current version of Egison has three special features.

First, it has a strong pattern-matching facility. We can describe pattern-matching against the wider range of data than the popular languages.

Second, it support symbolic computation as Mathematica. It is implemented utilizing Egison pattern-matching.

Third, it supports tensor index notation.

Let me explain all of these feature today. These features are useful to represent mathematical physics in programs.

#5

Here is a list of calculations of mathematics in Egison. I am listing up these programs on my website. This is the current list.

#6

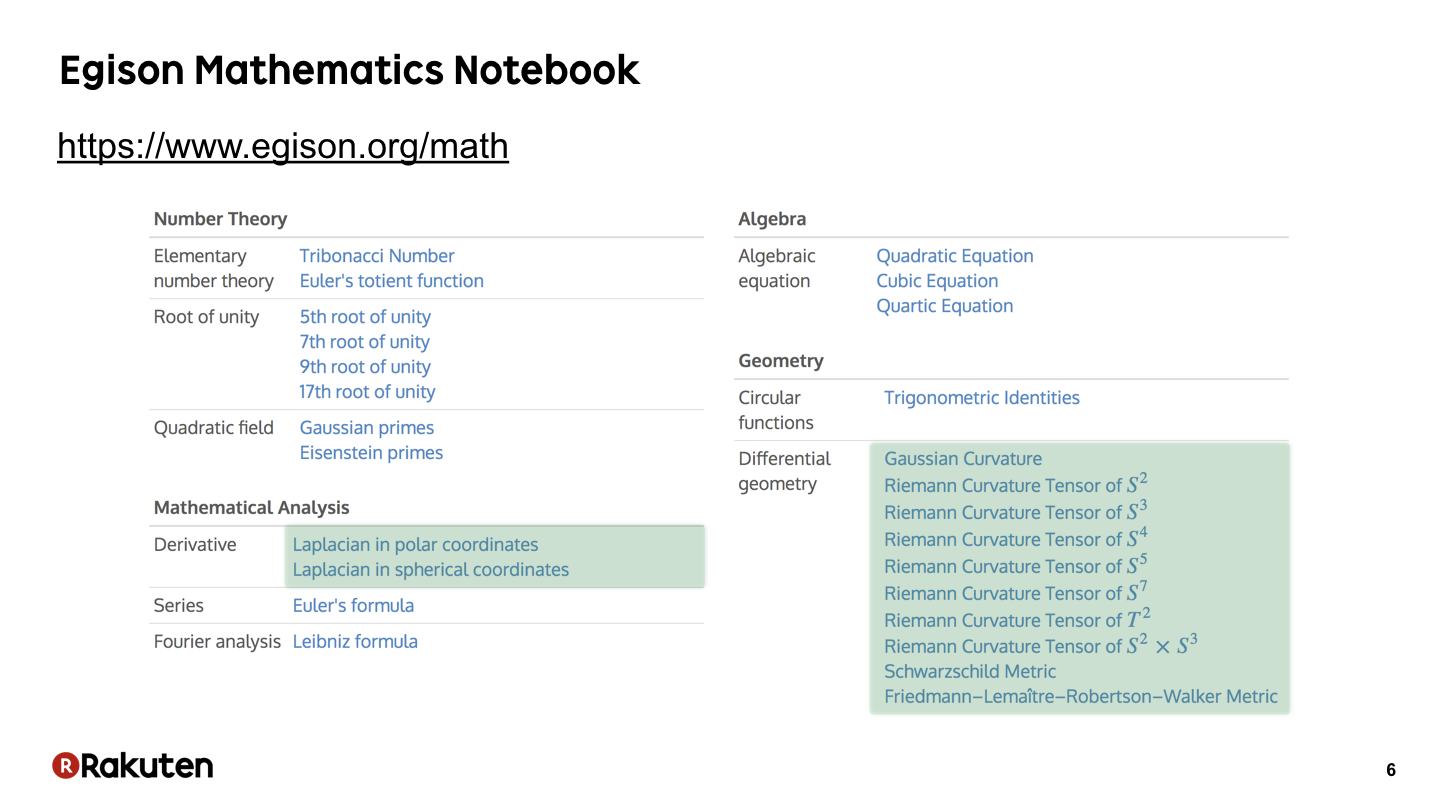
These green parts are programs for calculations of Riemannian geometry. That’s today’s topic.

#7

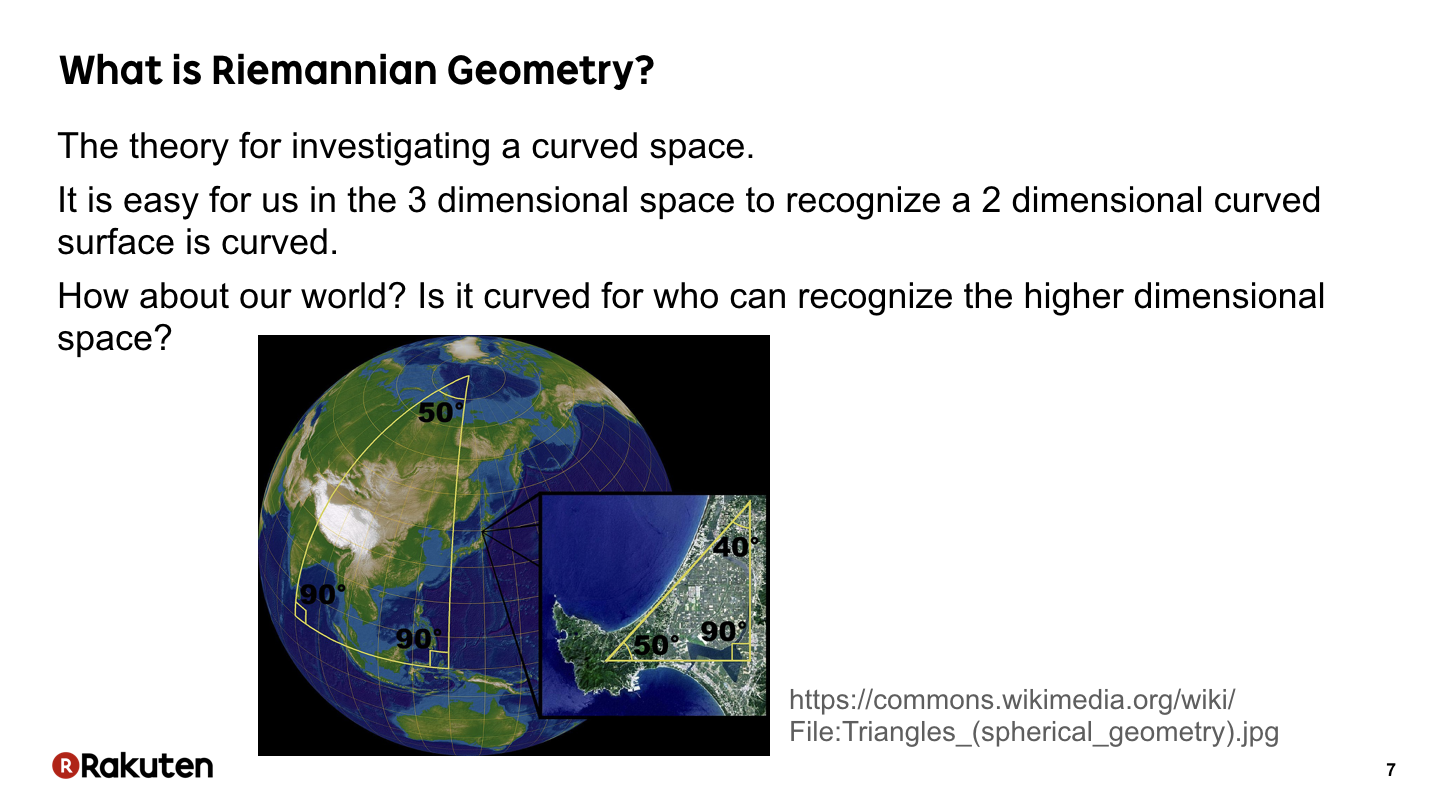
Before showing Egison program, let me explain what is Riemannian geometry. Riemannian geometry is the theory for investigating a curved space.

It is easy for us in the 3 dimensional space to recognize a 2 dimensional curved surface is curved. But how about our world? Is it curved for who can recognize the higher dimensional space?

Riemannian geometry provides a way for investigating our world is curved or not, by investigating our world inside itself.

#8

After the establishment of Riemannian geometry, Einstein built the theory by which we can explain the reason of gravity as a curve of 4 dimensional time-space. That is the theory of general relativity. This theory is described using the notion discovered in Riemannian geometry.

#9

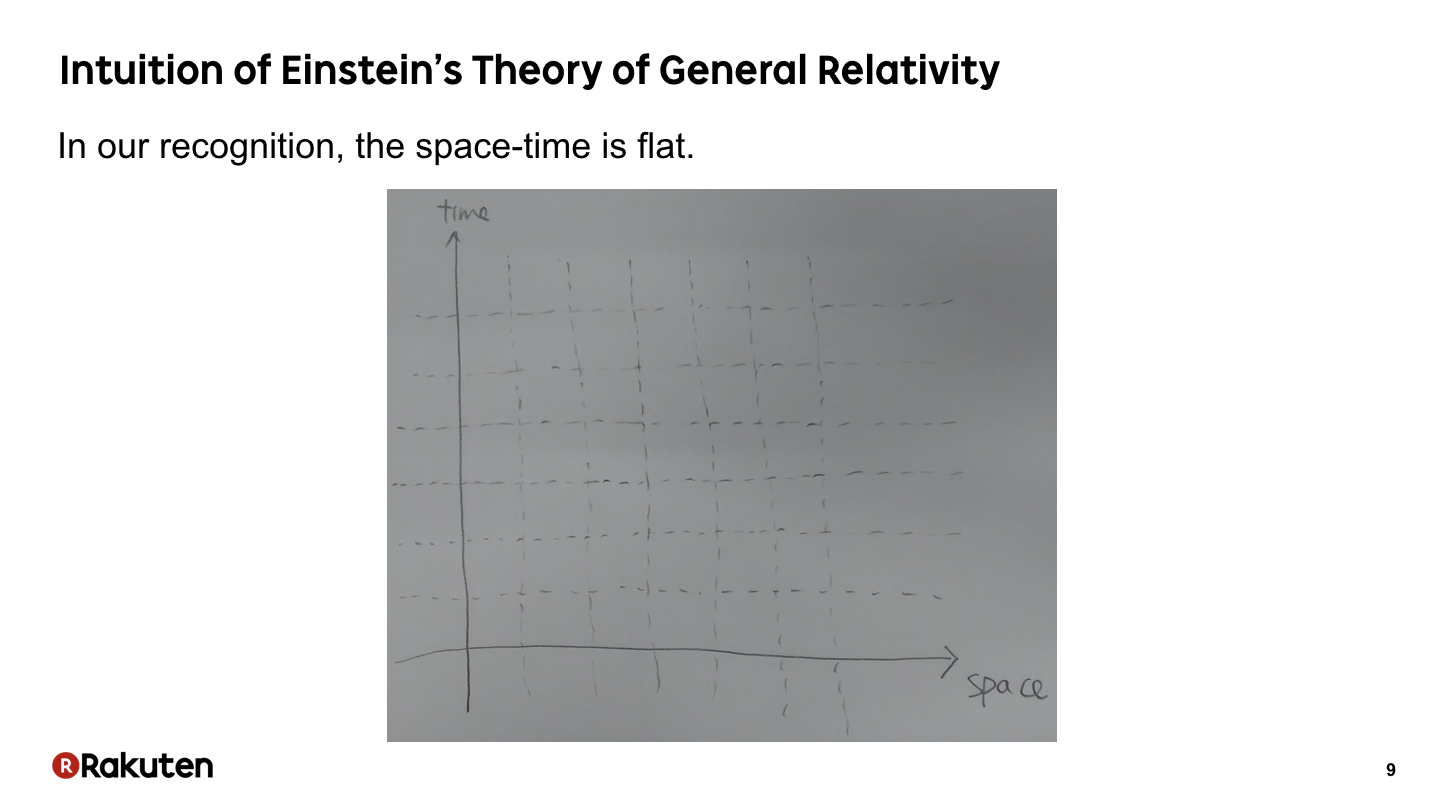
Let me show the intuition of the reason of gravity.

We recognize our space-time is flat, that way.

#10

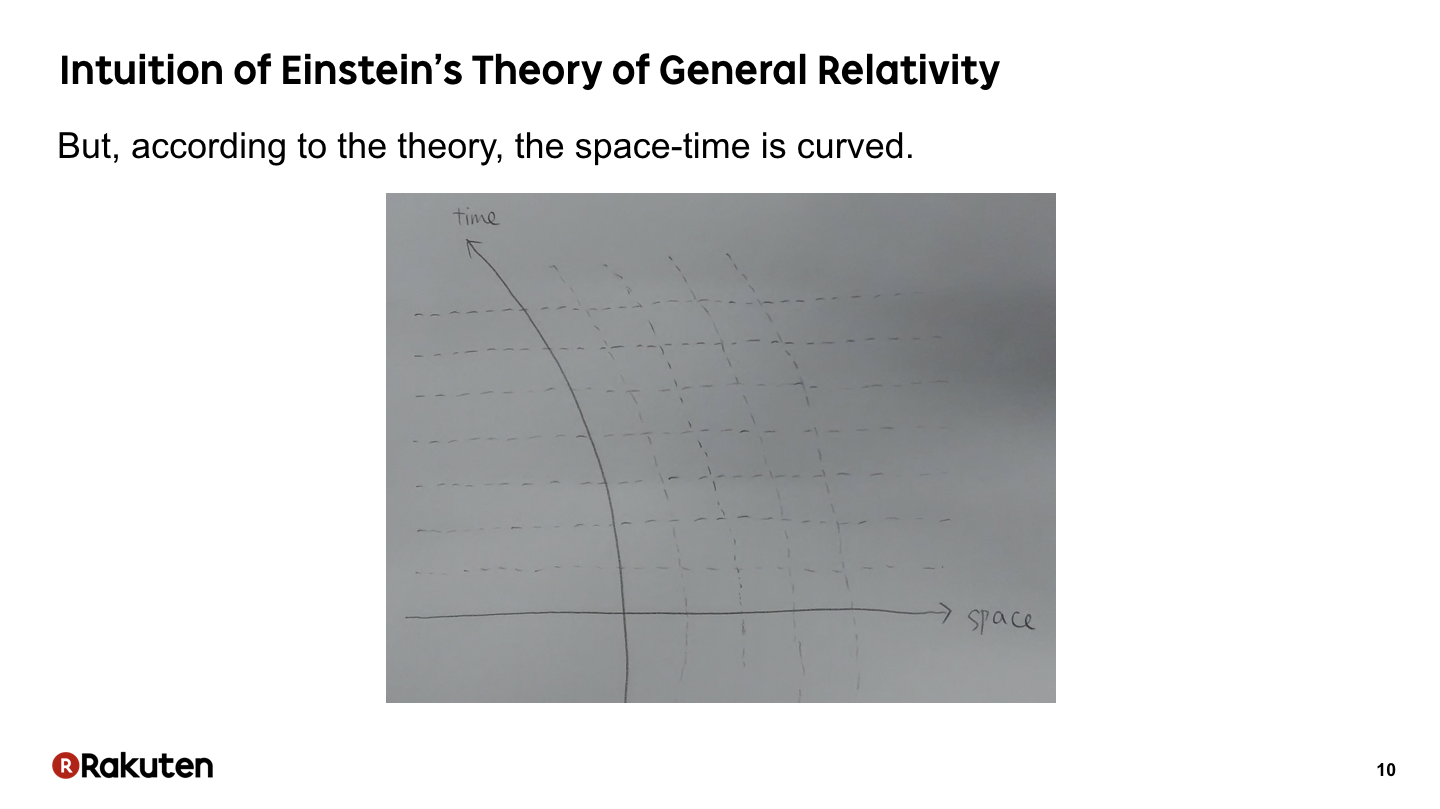
However, according to Einstein’s theory, our space-time is curved, that way. The line we recognize straight is curved for who can recognize higher dimension.

#11

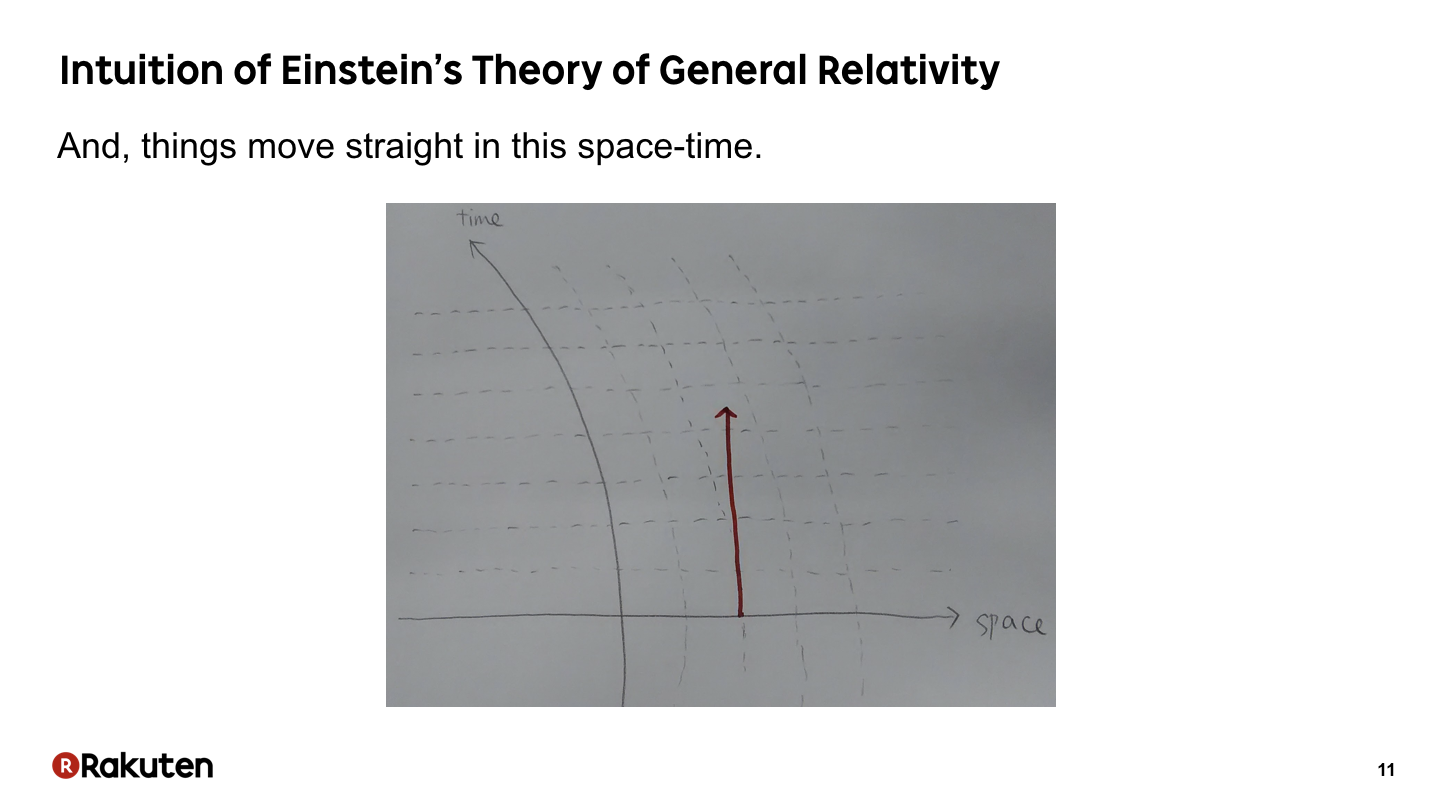
And things move straight in this space-time.

#12

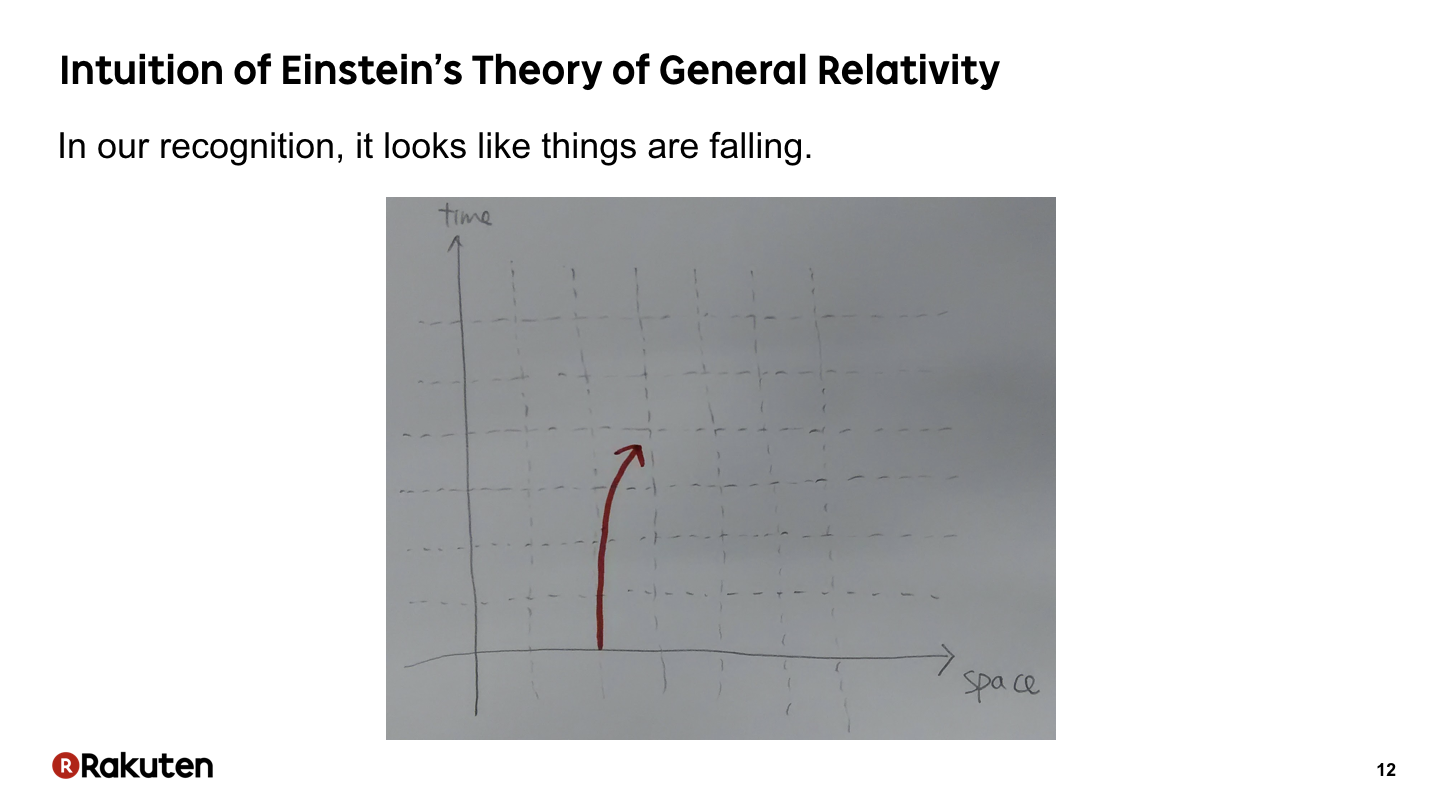
If we draw the straight line in the previous slide, the line is curved, that way. This curve corresponds to the drop of a thing. In our recognition, it looks like things are falling.

#13

Formulas in Riemannian geometry are represented with partial derivative operator and tensor index notation. And, actually, we can represent both of them concisely in Egison! Let me explain about that today.

#14

This is a sample of Egison representing the formula of Riemannian geometry. In Egison, we can directly translate the mathematical formula into a program. Please note that, we directly translate partial derivative operator and tensor index notation in this formula.

#15

These three features of Egison enable this concise notation. Now let me introduce these features.

#16

First, let me introduce pattern-matching against the wider range of data types.

#17

Here is a sample program of Egison pattern-matching. Egison allows non-linear pattern-matching with multiple results. Non-linear patterns are patterns that allow multiple occurrences of same variables in a pattern. Non-linear pattern-matching is one of the special feature of Egison pattern-matching.

The primes in this program contains the infinite list of prime numbers. We match against that as a list of integers. This is the pattern to match a twin-prime. “join _” discards head elements from the list of primes. With “cons $p”, we extract one prime and bind it to the variable p. “cons ,(+ p 2)” matches if the next prime after “p” is “p + 2”. Thus, the pattern matches with a twin-prime. In the body, we return “p” and “p+2”. The match-all expression returns all successful results of pattern-matching. Thus, it enumerates all twin primes.

Here, we extract the first 6 twin-primes.

#18

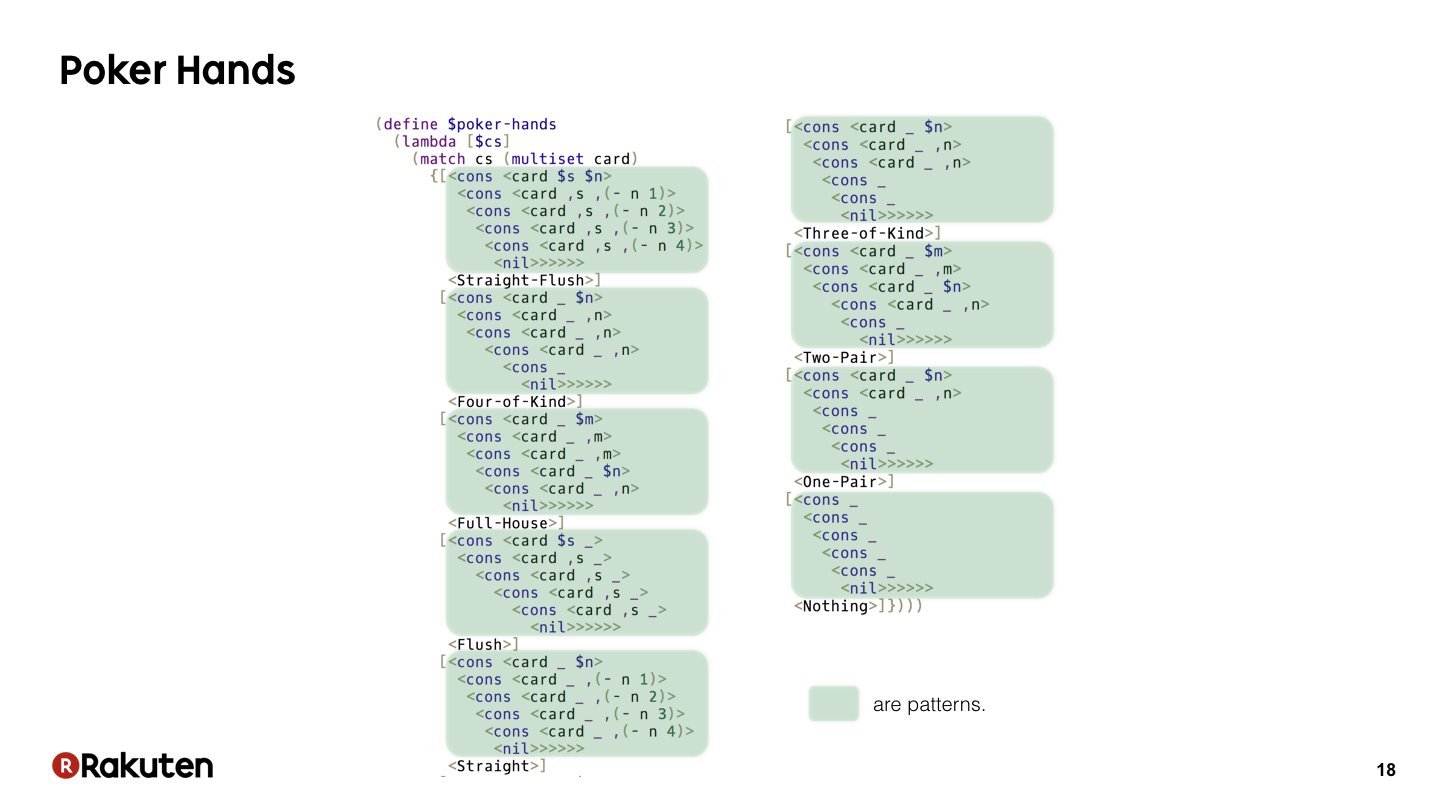
The speciality of Egison pattern-matching is that we can represent pattern-matching against wider range of data types. For example, we can represent pattern-matching against multisets as this sample. We can write a program to determine poker hands very concisely if we combine pattern-matching against multisets and non-linear patterns. Actually, the method for pattern-matching against multisets is defined in Egison. So users can define it by themselves.

#19

Next, let me introduce the second feature, customizable symbolic computation using Egison pattern-matching.

#20

First, let me show what is symbolic computation. In symbolic computation, we can use symbols such as x, y, and i, that way.

In the first expression, we describe “x plus y powered by 2”. It returns “x powered by 2 plus 2 x y plus y powered by 2”.

In the second expression, we describe “x plus y powered by 3”. In the third expression, we describe “x plus y powered by 4”.

In the fourth expression, we describe “1 + i powered by 4”. This i is a unit of imaginary number. It returns “-4”.

In the fifth sample, we describe “square root of 4”. It returns “2”.

In the sixth sample, we describe “square root 2 multiplied by square root 3”. It returns “square root 6”.

We can describe such kind of calculation in programs in programming languages that support symbolic computation.

#21

If we combine Egison pattern-matching and symbolic computation, we can define the symbolic partial derivative in a very concise program.

Here is a program that defines the symbolic partial derivative in Egison. Pattern-matching against mathematical expressions is utilized to define that. A mathematical expression is a multiset of terms. A term is a multiset of factors. So pattern-matching against mathematical expression can be described concisely in Egison that way.

#22

Now, let me introduce the third feature, tensor index notation in Egison.

#23

First, let me show what is tensor index notation.

Tensor index notation is a popular notation in the field of mathematics and physics. Here are formulas from Riemannian geometry. We can see many indices are used in the formulas.

#24

These are the simplest samples of tensor index notation. We represent inner-product, Hadamard product, and tensor-product of two vectors by just changing the index. In index notation, the position of the index has meaning. As the first sample, when the index is repeated in a superscript and a subscript, it contracts the components. That is, it calculate the inner-product. As the second sample, when the index is repeated in the same position, each component of vectors are multiplied. As the third sample, when the indices are different, the tensor-product of two vectors are calculated. That way, we can control the way of multiplying vectors.

#25

We can append multiple indices to the high-order tensors. In this sample, we represent multiplication of matrix using index notation. Index notation is necessary to represent the multiplication of the higher-order tensors than matrices, because there are many ways to transpose them.

#26

This is a sample program of Egison using tensor index notation. The program below represents the above mathematical formula. In Egison, we represent superscripts with the “~” sign and subscript with the “_” sign.

#27

These are programs that represent the same formula in Wolfram and Egison.

Please note that a double loop consisting of the Table and Sum expressions appears in the program in the Wolfram language, whereas the program in Egison is flat, similar to the mathematical expression. This is achieved by using tensor index notation in the program.

Egison expresses mathematical expressions more directly than the Wolfram language, though there is little difference in the number of lines in the programs.

#28

Actually, I published a paper that explains a method for importing tensor index notation into programming. Please read that if you have interest.

#29

Now, let me show you how we can describe the calculation of the Riemannian curvature tensor as an sample application of Egison.

#30

Actually, we can write a program to calculate the Riemann curvature tensor of the surface of a sphere in one slide.

#31

In this part, we set the parameters and calculate the local basis.

#32

In this code, we calculate Riemann metrics of the surface of a sphere.

In Egison, we can specify the type of indices in the variable name when binding a tensor to a variable. For example, we can bind different tensors to “g__” and “g~~”.

#33

Here, we calculate Christoffel symbols of the first kind. Tensor index notation is effectively used to represent the formula.

#34

Here, we calculate Christoffel symbols of the second kind. The formula is directly represented.

#35

This is a part of the program that is representing the formula of Riemann curvature tensor.

#36

We can also describe the calculation of the Ricci and scalar curvature concisely.

#37

Here is a program that describe the calculation of the general theory of relativity. This program calculates the Riemann curvature tensor of Schwarzschild space, the space-time where there is only one star in the origin. If we analyze the result of this program, we can see the reason of gravity geometrically.

Actually, I found the proposed method when I was trying to implement this calculation as concisely as possible extending Egison.

#38

Finally, let me talk about my future plan.

#39

Currently, I am working to represent mathematical notions that are important in gauge theory, such as differential forms, exterior derivative, and Hodge operator. If we use these notions, we can represent formulas in mathematical physics more concisely as this. Gauge theory is a theory in physics that appeared after Einstein’s theory of general relativity. If we achieve that, there are the wider range of application in research of mathematics, physics, and computer simulation.

#40

That is today’s topic. Thank you very much for your attention. I am happy to hear for your questions now.

Article List

Recent Tweets

This website in other langauge: English, 日本語