APLAS 2018 Presentation: Non-linear Pattern Matching with Backtracking for Non-free Data Types
At APLAS 2018, we made a paper presentation on Egison pattern matching system. The following are our slides and script. We can download our paper from Springer and arXiv.
#1

Good morning everybody. Thank you for inviting us today. I am happy to be here. Today, I'd like to talk about our new pattern-matching system for non-free data types.
#2

First, let me explain our motivation.
#3

The aim of our research is to create a programming language with an expressive pattern-matching facility for non-free data types. We would like to achieve pattern matching like regular expressions for arbitrary user defined data types including non-free data types.
#4

Let me explain what are non-free data types. Non-free data types are data types whose data have no standard form. For example, a multiset is non-free data types, because a collection {a, a, b} has two equivalent but different forms {a, b, a} and {b, a, a}.
Basically, free data types are data types that can be represented as algebraic data types. For example, consed lists and syntax trees of programming languages are free data types.
The other data types are non-free data types. For example, multisets, sets, graphs, and mathematical expressions are important non-free data types.
(List with join constructor is also a non-free data type. This is because it also has multiple representation for an equivalent datum, that way.)
Our motivation is to extend the range of data types that we can use pattern matching to these non-free data types. It enables us to describe many algorithms more concisely than now.
#5

There are many existing work for pattern matching against non-free data types. Here are the list of these work. Let me classify them by their features.
#6
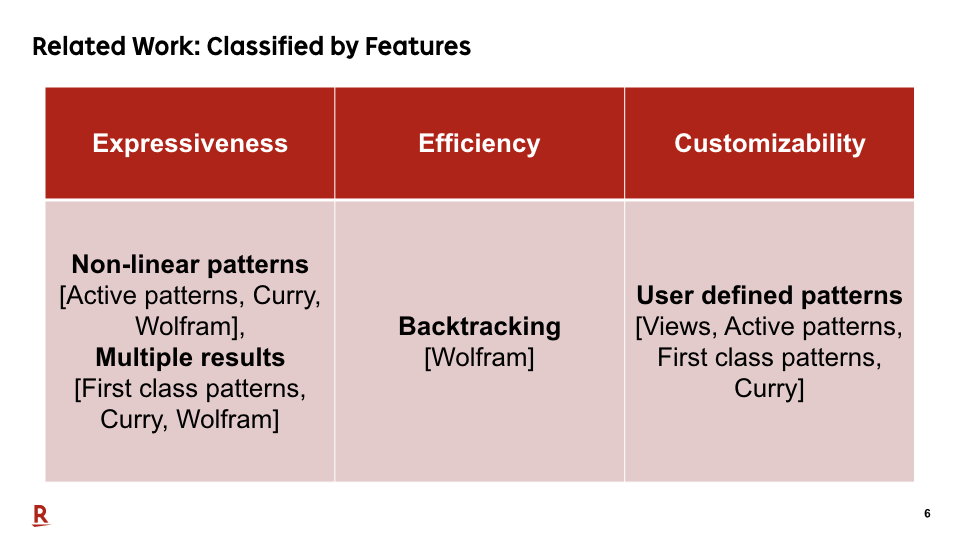
This table shows the classification. We listed all the features proposed by the existing work and listed the existing work that satisfy each feature. We explain each existing work from the next slide.
#7
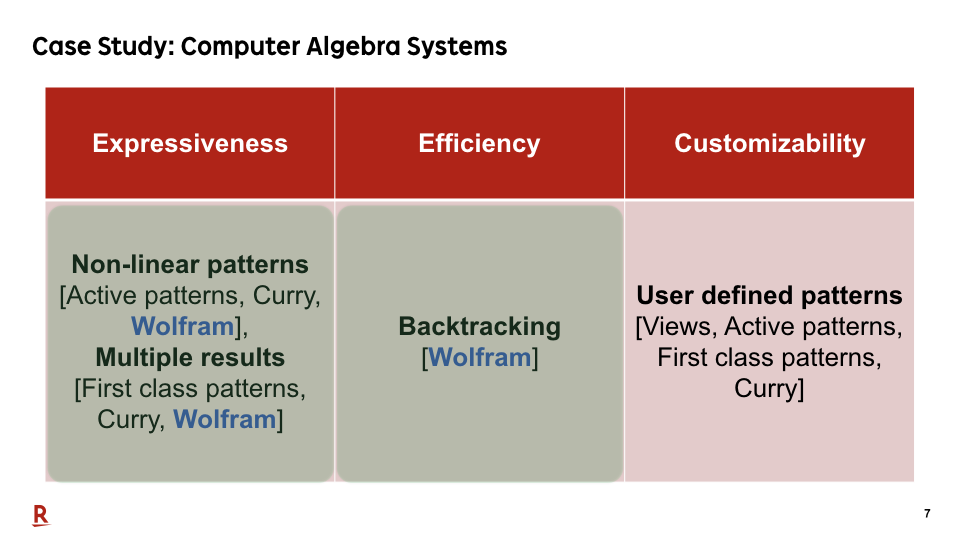
Let me start with the pattern-matching of computer algebra systems.
Most of computer algebra systems have an practical pattern matching engine for mathematical expressions. They support both non-linear patterns and backtracking. Non-linear patterns are patterns that allows multiple occurrences of the same variables in a pattern. Computer algebra system can process non-linear patterns efficiently by backtracking.
However, their disadvantage is extensibility. These pattern-matching engines are specialized only for well-known mathematical structures. Users cannot extend the pattern-matching algorithms by themselves.
#8
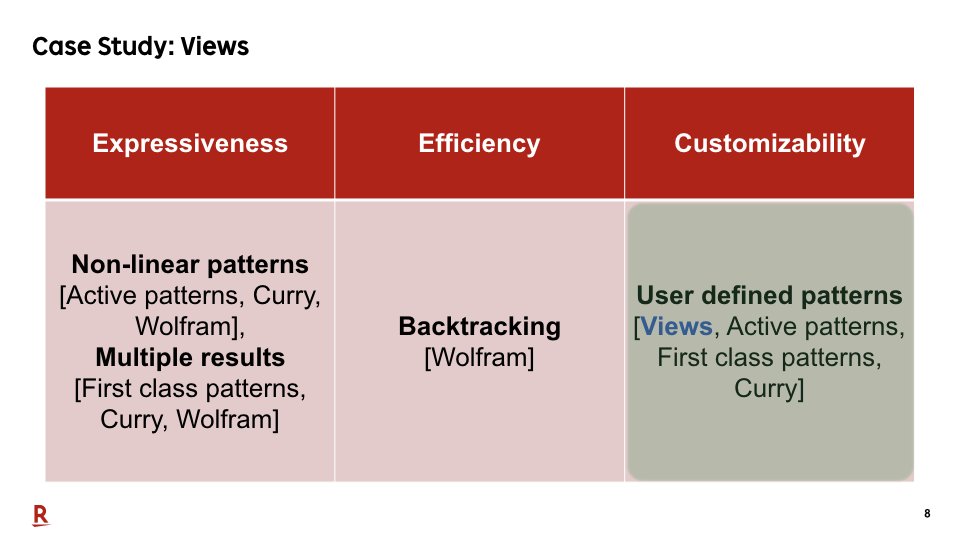
Wadler's views are an earlier research that allows users to extend the pattern-matching method for each pattern. However, views support neither non-linear patterns and pattern matching with multiple results. Therefore, we cannot describe expressive patterns.
#9
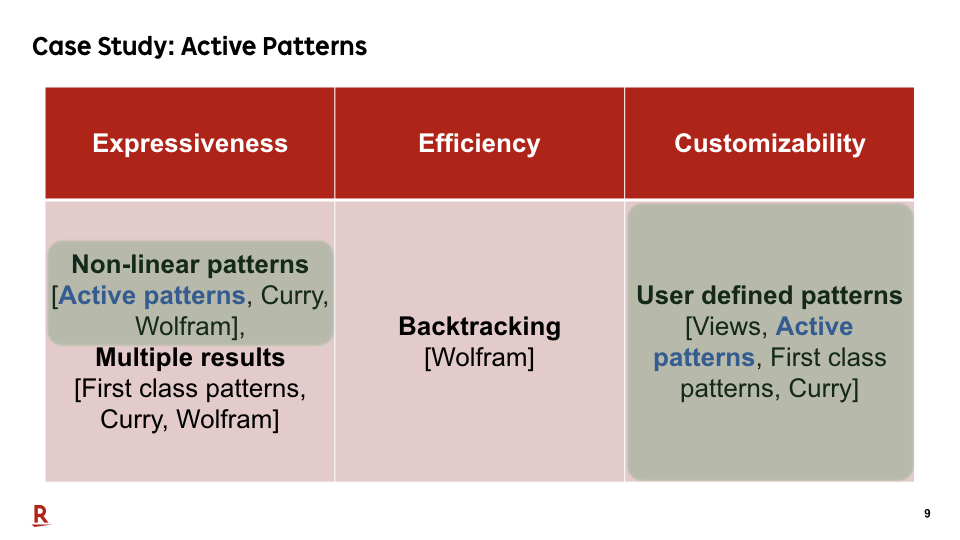
Active patterns are an extension of views that support non-linear patterns. However, it does not support pattern matching with backtracking. Therefore, we cannot still describe expressive patterns.
#10

This is an example of active patterns. Add' is a pattern constructor defined using active patterns. It matches if the target collection contains the first argument of Add'. This pattern constructor extracts one element from a collection as a multiset, ignoring the order of the elements.
#11

We can use this pattern for defining the member function only with pattern matching.
#12

However, for example, we cannot describe a pattern that matches the collections that contain a pair of identical elements. This is because active patterns do not support backtracking.
#13
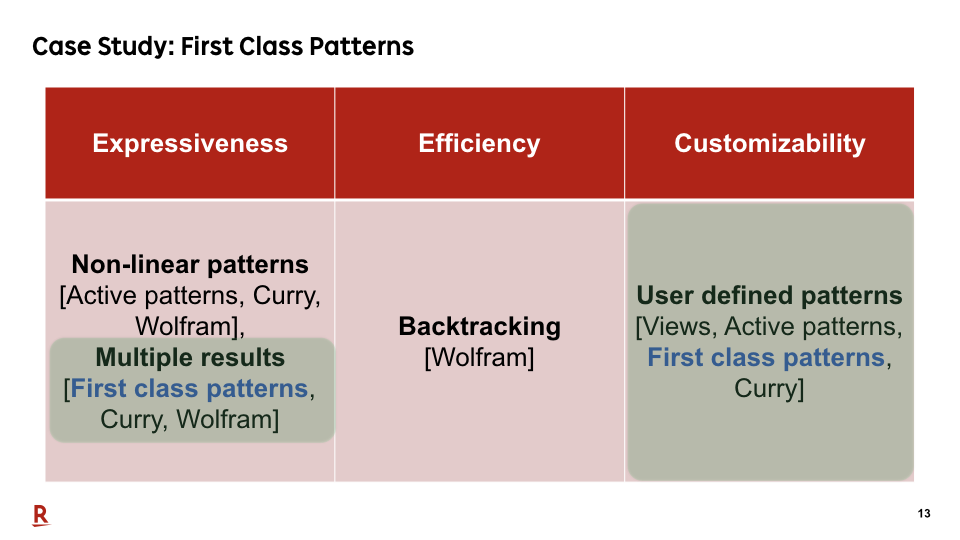
First class patterns are another extension of views that support pattern matching with multiple results. However, First class patterns do not support non-linear patterns. Therefore, we cannot still describe expressive patterns.
#14
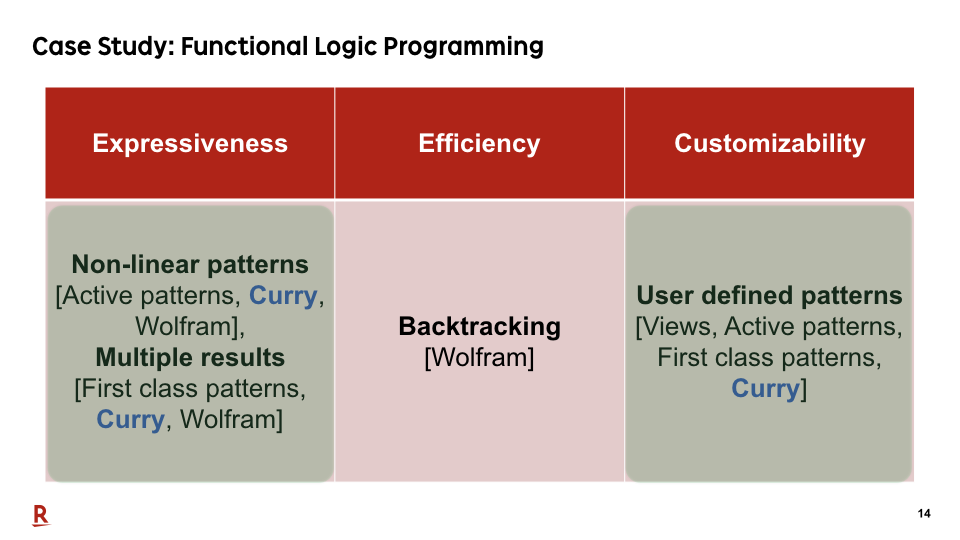
Functional logic programming is an independent approach for non-free data types. It supports both of non-linear patterns and multiple results. So we can describe expressive patterns using it. However, the current implementations of functional logic programming languages do not handle non-linear patterns efficiently.
#15

Let me show an example.
This is a sample program of Curry, the most popular functional logic programming language. insert is a pattern constructor defined in Curry. This pattern constructor extracts one element from a collection as a multiset, ignoring the order of elements, like Add' in the previous example.
#16

Here are patterns for finding sequential pairs, triples, and quadruples from a collection. We can describe them concisely using non-linear patterns.
#17

However, non-linear pattern matching is not efficiently executed in Curry. Theoretical time complexities depend on the size of patterns, that way. Here are the benchmark results.
#18

The reason for the difference of time complexity between these patterns is because Curry transforms non-linear patterns into pattern guards. Basically, pattern guards are applied after enumerating all pattern-matching results. Therefore, substantial unnecessary enumerations often occur before the application of pattern guards.
#19

Another key difference with the functional logic programming and the others is the method for defining the pattern-matching algorithms for each pattern. In this approach, we describe pattern-matching algorithms in logic-programming style. A pattern constructor takes decomposed values and returns the target data in its definition. On the other hands, in the functional approach, a pattern constructor takes a target and returns the decomposed values. In logic-programming style, it is difficult to directly describe efficient pattern-matching algorithms.
#20
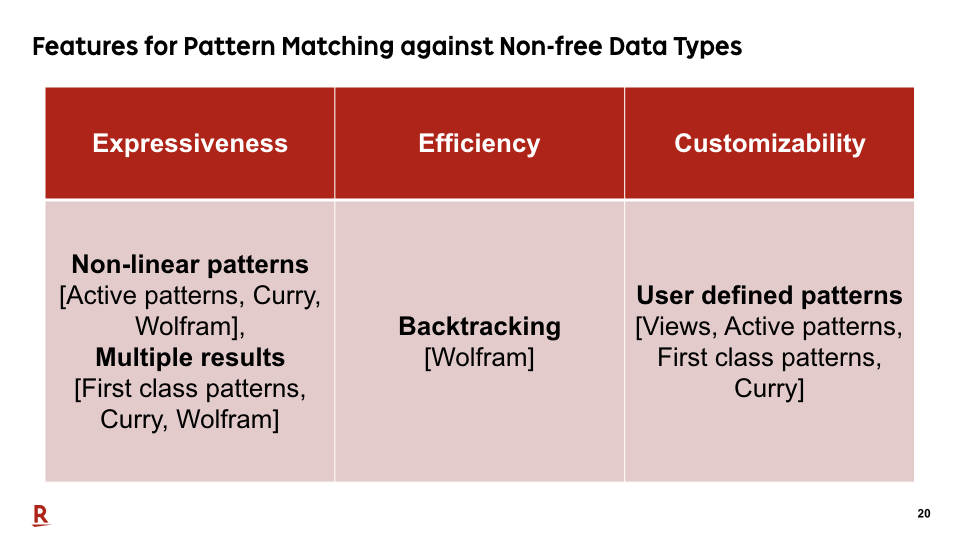
As we have seen so far, all the features in this table are important for pattern matching against non-free data types. However, there is no existing research that supports all the features in this table.
#21
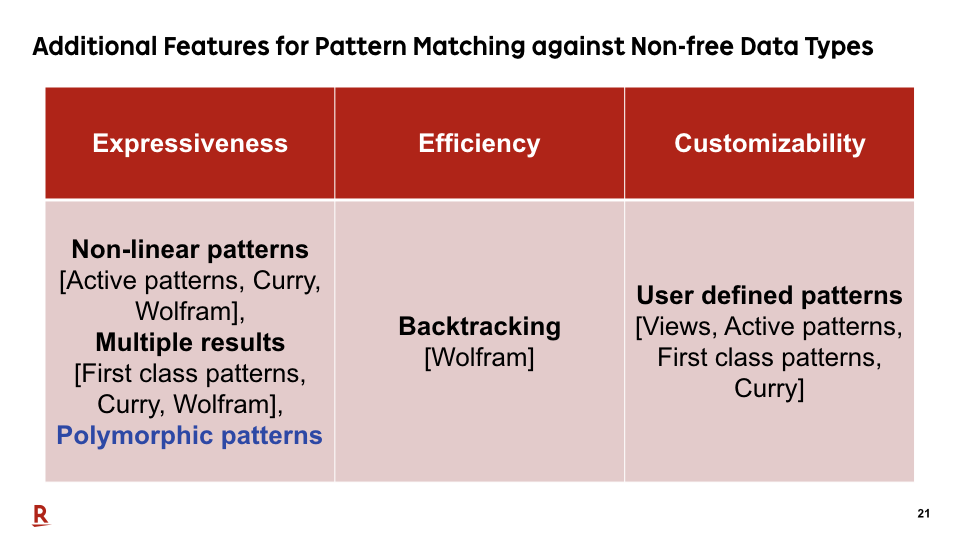
Furthermore, in our paper, we additionally proposed this feature, polymorphic patterns, for practical pattern matching against non-free data types. Let me explain what are polymorphic patterns.
#22

This is a sample program to show the importance of polymorphic patterns.
Polymorphism is important especially for value patterns. A value pattern is a pattern that matches when the value in the pattern is equal to the target. It is an important pattern construct for expressing non-linear patterns.
If patterns are monomorphic, we need to have different notations for value patterns for lists and multisets as this sample. This is because both lists and multisets are represented as a list, but the equivalence of them are different.
#23
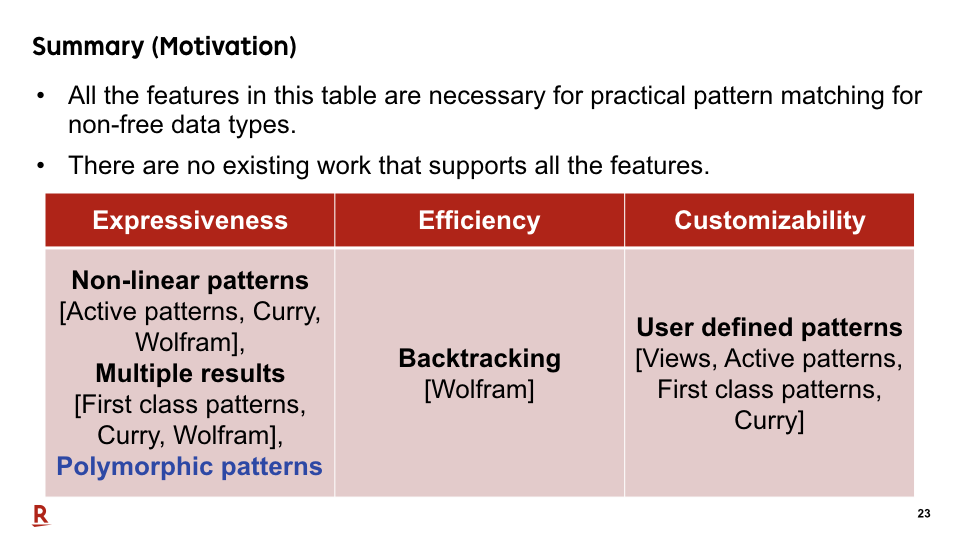
Let me summarize my presentation so far. We made two claims. The first claim is that all the features in this table are necessary for practical pattern matching for non-free data types. The second claim is that there are no existing work that supports all the features.
#24

Now, let me explain our solution.
#25
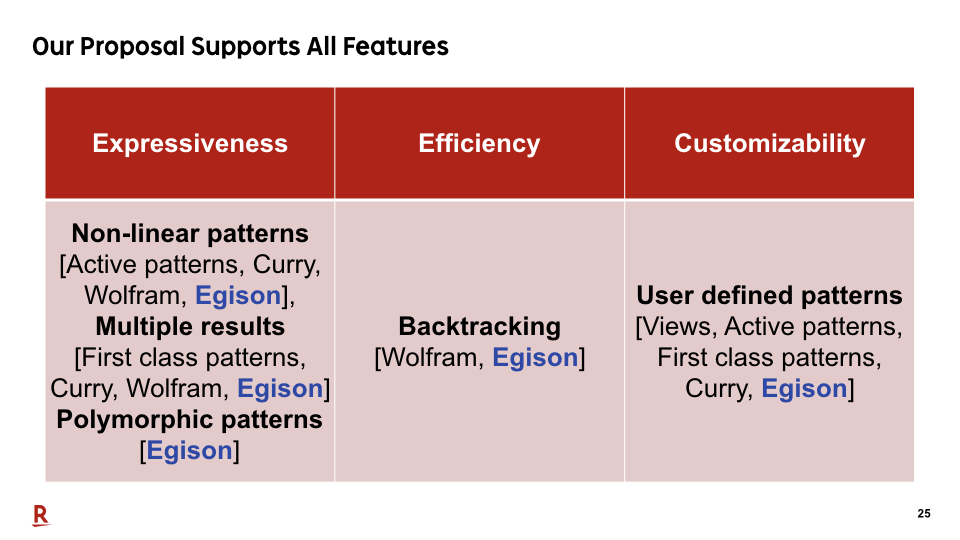
We've designed a pattern-matching system that supports all these features and implemented it on our proof-of-concept language Egison.
#26

Let me explain how we achieve that.
#27
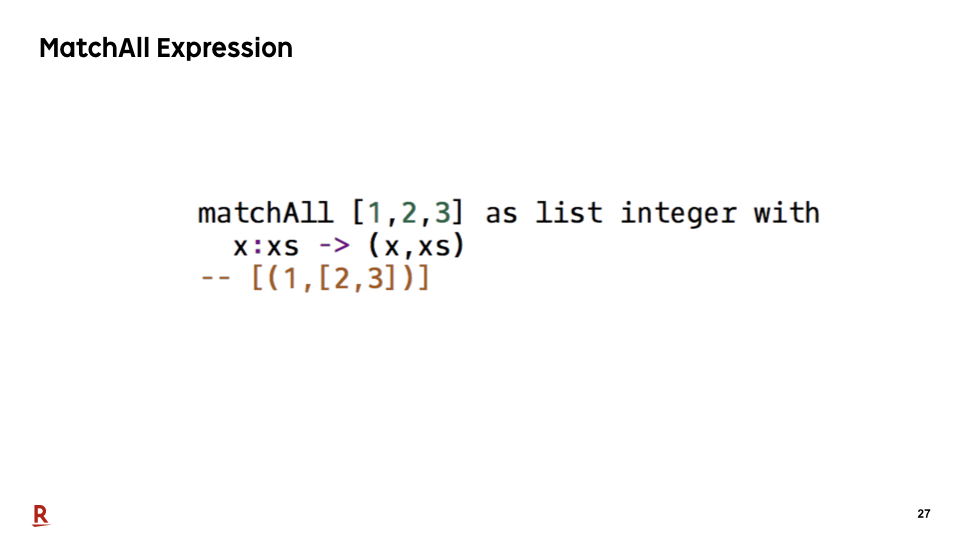
First, let me show our pattern-matching expression. By the way, current implementation of Egison has Lisp-like syntax. But in this presentation, we use Haskell notation to omit the explanation of its basic syntax.
#28

MatchAll is a pattern-matching expression of Egison.
#29

MatchAll takes a target, pattern, and body as the match expressions of the other languages.
#30
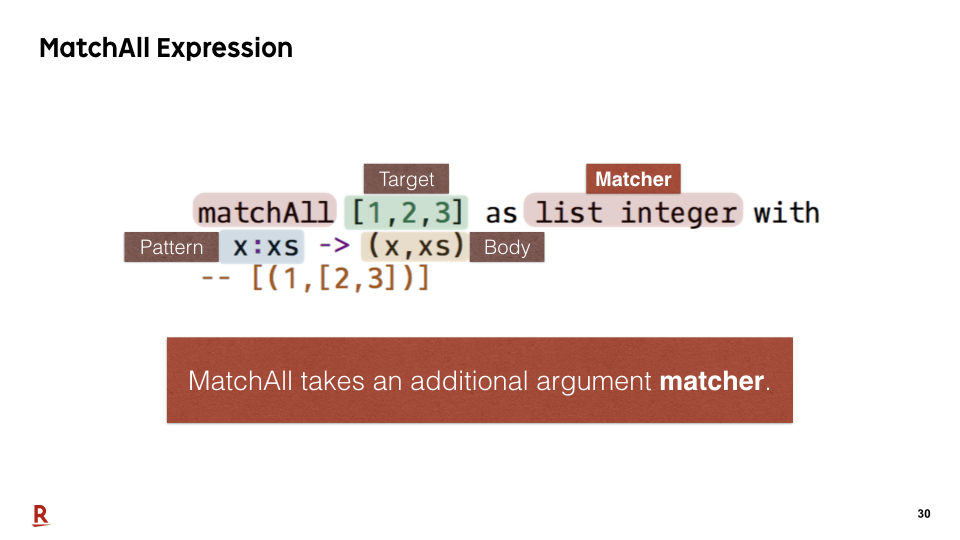
MatchAll takes an additional argument matcher.
#31

As we have seen, this pattern-matching expression has two characteristic parts: the name of syntax matchAll and a matcher.
#32

First, let me explain the reason of the name matchAll.
MatchAll returns a list of all pattern-matching results. Generally, pattern matching for non-free data types has multiple results. So this expression is often useful for handling them.
In this case, there is only one decomposition. So, the returned list contains only one element (1,[2,3]).
#33

Next, let me explain what is a matcher. A Matcher is an Egison specific object that specifies the pattern-matching method.
#34

If we pass a different matcher to a matchAll expression, the different pattern-matching methods are executed. The multiset matcher ignores the order of the elements in a collection. Therefore, in this case, there are three decompositions [(1,[2,3]), (2,[1,3]),(3,[1,2])].
#35

In fact, these matchers, list and multiset, are defined by users in Egison. Let me explain how we can define them.
#36

This is a definition of the list matcher.
#37

Each part of this program defines a pattern-matching method for each pattern.
#38

These parts are patterns for pattern. The structure of the matcher expression is similar with the match expression of the existing languages.
#39

Definitions of each pattern are similar with the definition of pattern constructors in existing functional approach for non-free data types. A difference from the existing work that I'd like you to notice about this matcher expression is that it modularizes pattern-matching method for each data type, not for each pattern.
#40

The multiset matcher is defined in a similar way. We come back here later again.
#41

Thanks to the design of our matchAll and matcher expression, we achieved the polymorphic patterns, that way. We can use the same pattern constructor names "cons" for different matchers.
#42

Let me proceed to the next phase.
#43

We've also achieved the polymorphic value patterns. We can write the value patterns in the same notation.
Here, we are checking the equality of a collection [1,2,3] as a list and multiset, respectively. The pattern is [2,1,3]. If we regard it as a list, they are not equal. But if we regard it as a multiset, they are equal. So, in this case, only the second expression succeeds in pattern matching.
#44

It is achieved by defining the pattern-matching method for the value patterns in a matcher, that way.
#45

This is a definition of the pattern-matching method of the value patterns for multiset. The modularization of pattern-matching method by matchers, not by patterns, allows us to achieve polymorphic value patterns.
#46

Now, let me proceed to the third phase.
#47

Let's see how the pattern-matching method is defined for the cons pattern of multiset.
#48

The definition of pattern-matching method is divided into three parts. First, the pattern for patterns. Second, the next matcher expression. Third, the next target expression.
This pattern for patterns contains two dollar signs. It means the cons pattern takes two patterns as arguments and these two argument patterns become next patterns.
This next matcher expression returns a tuple, m and multiset m. m is a matcher for inner element of the multiset. It means the first argument of the cons pattern is matched as an inner element, and the second argument is matched as a multiset, recursively.
This next target expression returns the target, that way, when the target is a collection [1, 2, 3]. In this expression, matchAll is effectively used for this decomposition.
#49

Now, let me explain the pattern-matching algorithm inside Egison by showing what happens when we execute the above pattern-matching expression.
Pattern matching algorithm of Egison is designed as a reduction of data, called matching states. A matching state is a datum that consists of stack of matching atoms, and intermediate pattern matching results.
#50
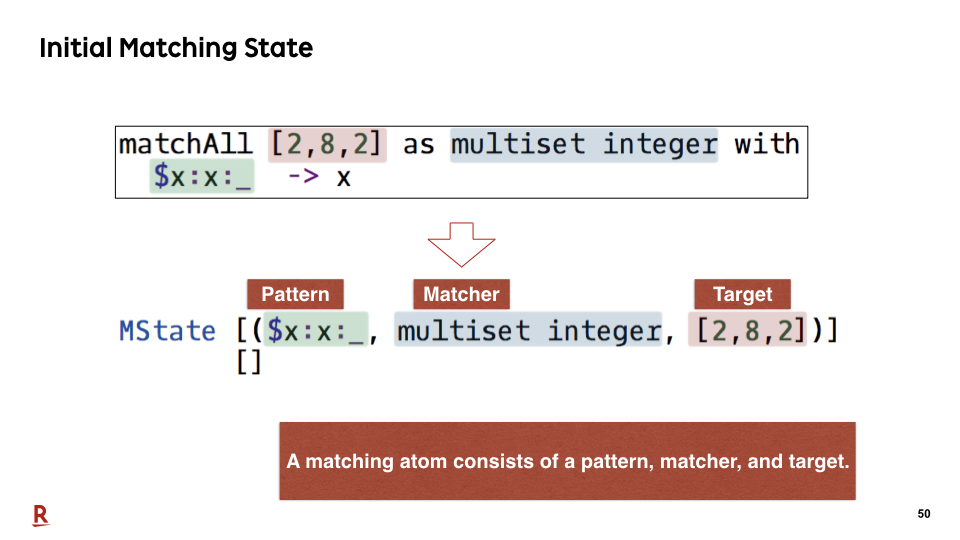
A matching atom consists of a pattern, matcher, and target. From this matchAll expression, the initial matching state is created, that way.
#51

Reduction is executed recursively referring to the definition of the matcher. In this case, the next matching states are generated from the definition of the cons pattern in the multiset matcher that we've seen in the previous slide.
#52

In this presentation, we examine the reduction of only this matching state.
#53

In the next step, the matcher of top matching atom changes from integer to something. This reduction is defined in the integer matcher.
#54

In the next step, a new binding is added to the intermediate pattern-matching result. something is the only built-in matcher in the proposed system, which can add a new binding to the intermediate pattern-matching result, that way.
#55

In the next step, two matching states are generated by the cons pattern of the multiset matcher.
#56

The first matching state fails for pattern matching of the value pattern and vanishes because 8 is not equal to 2.
#57

Let's examine the reduction of this matching state.
#58

In the next step, the value pattern matches with the target and the matching atom is popped out.
#59

In the next step, the matcher changes from multiset integer to something.
#60
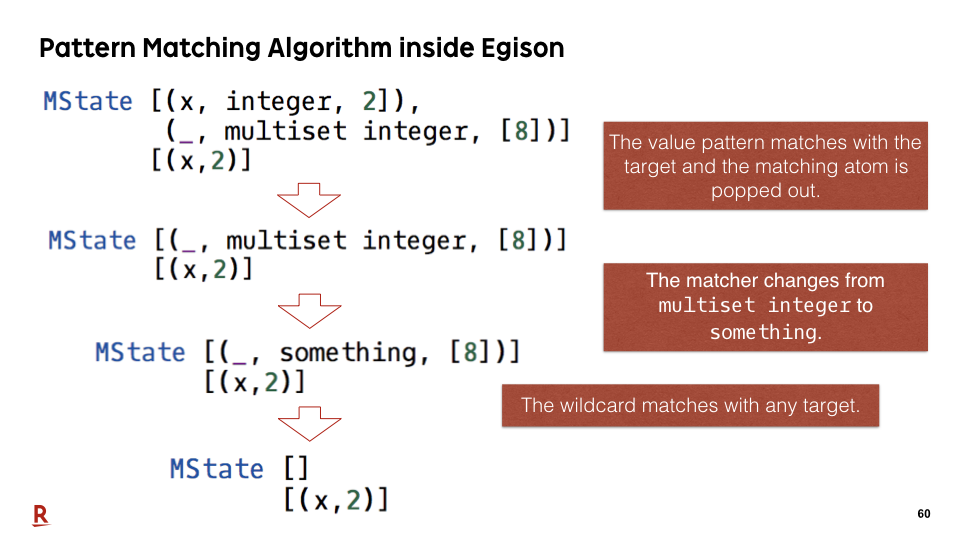
In the next step, the wildcard matches with the target, and the top matching atom is popped out.
#61
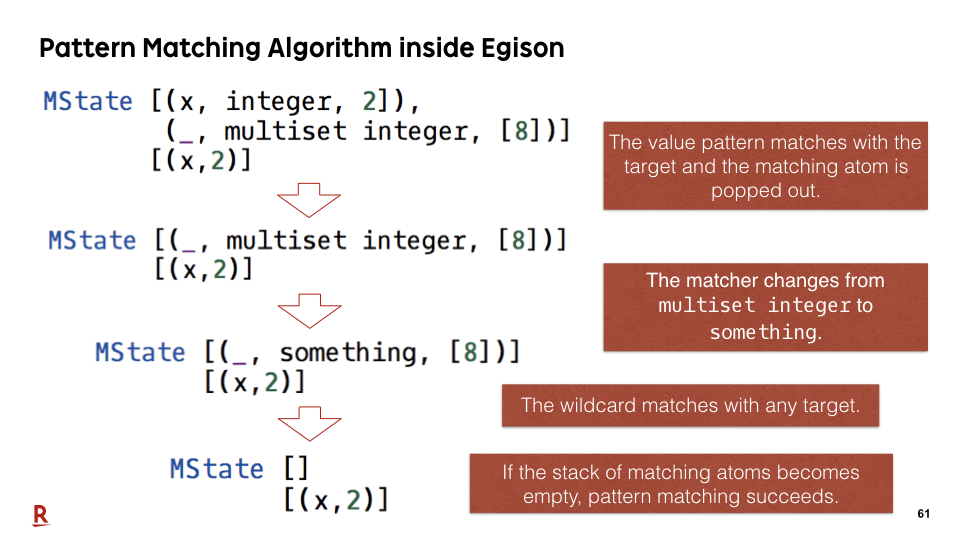
Finally, if the stack of matching atoms becomes empty, pattern matching succeeds.
#62
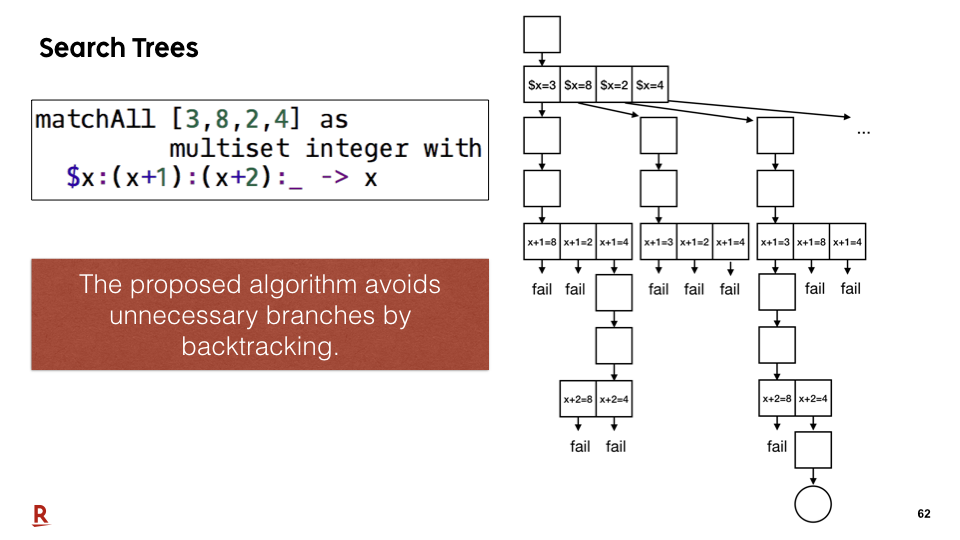
Let me show the search trees for non-linear pattern matching in our proposal. The nodes of this tree represent matching states. The proposed algorithm avoids unnecessary branches by backtracking, that way.
#63

Therefore, theoretical time complexity of non-linear pattern matching does not depend on pattern size. We do not write special algorithm for that in the matcher definition. Algorithm described in the matcher definition is similar with the existing work.
This efficiency is achieved by the runtime algorithm inside Egison. Of course, if users optimize the matcher definition, pattern matching will be much more efficient.
#64

Finally, let me talk about matcher compositions. The proposed recursive pattern-matching algorithm enables us to compose matchers.
#65

As in this sample, we can compose matchers and create new matchers. For example, we can create a matcher for a multiset of multisets.
Let me explain why we can compose matchers.
#66

In fact, list is defined as a function that takes a matcher and returns a matcher.
#67

multiset is also defined as a function that takes a matcher and returns a matcher.
#68

We can define a matcher for graphs and mathemtaical expressions by just composing matchers, that way. For example, an adjacency graph consists of a collection of adjacency lists. Therefore, adjacency graphs can be defined as a multiset of tuples of integer and a multiset of integers, that way.
#69

Here is a sample program that uses a matcher for adjacency weighted graphs. This matchAll lists all cycles that visits all cities and backs to Wellington.
#70
Egison has an interpreter implemented in Haskell and is open-sourced. Please try it.
#71

Now, let me summarize our talk.
We proposed the three criteria for practical pattern matching for non-free data types: Non-linear pattern matching with backtracking, extensibility of patterns, and polymorphic patterns. It is achieved by properly designing the matchAll, matcher, and pattern-matching algorithm. We have implemented our design as a proof-of-concept programming language Egison.
#72

These are topics we do not cover in this presentation. Please refer to our paper for the further information.
#73

Finally, let me talk about future direction.
#74

We have designed loop patterns that are extension of Kleene star operators of regular expressions for non-free data types. We want to pattern-match not only lists but also trees and graphs. So we had to extend Kleene star operators for them. I presented a paper on the loop patterns at Scheme Workshop 3 months ago.
#75
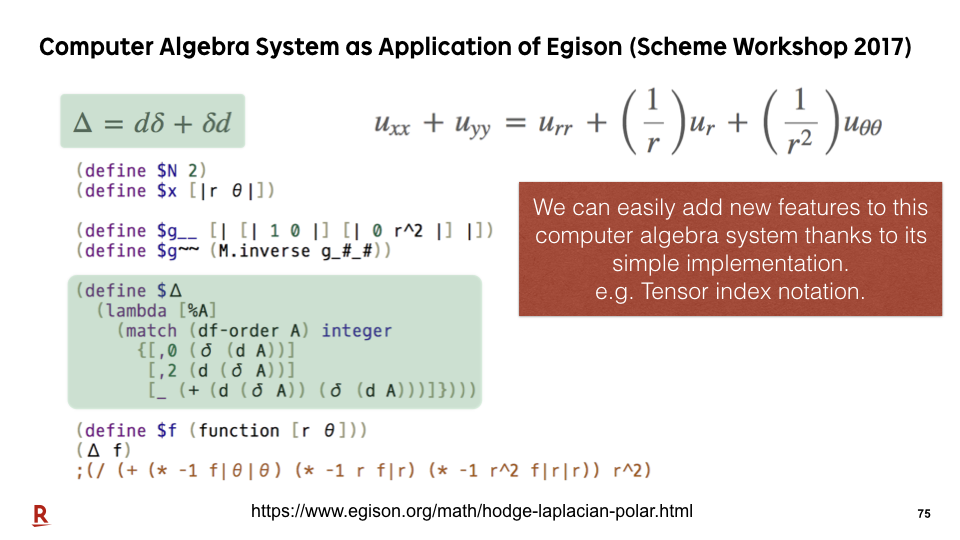
As an application of our proposed pattern-matching system, we have implemented a computer algebra system on Egison. We can implement a pattern-matching engine for mathematical expressions in very simple code. Therefore, we can try to implement new ideas on Egison more easily than the existing computer algebra systems. Last year, I presented a paper at Scheme Workshop for one of new features in Egison, tensor index notation, implemented on this computer algebra system.
#76
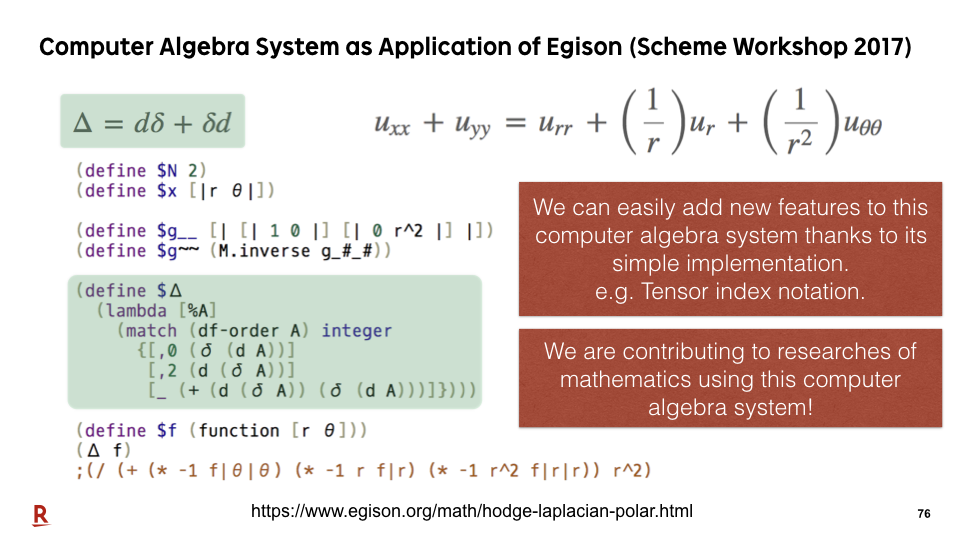
This computer algebra system can be used even for practical purpose. We have been already contributing to researches of mathematics using this computer algebra system.
#77

As a succeeding work, we are now trying to establish new programming style called pattern matching oriented programming style. Here is a list of functions we can define more elegantly using the proposed pattern-matching facility.
#78

Currently, Egison is a dynamic typed programming language. But, we have designed typing rules for Egison pattern-matching expressions. We are implementing a static type system for Egison and a GHC extension.
#79

That's today's topic. Thank you for your attention.
Article List
- APLAS 2018 Presentation: Non-linear Pattern Matching with Backtracking for Non-free Data Types [2018/12/03]
- Egison Presentation for Rakuten Technology Conference 2017 [2017/10/31]
- Egison Presentation for the Scheme and Functional Programming Workshop 2017 [2017/09/16]
- Egison Presentation for Rakuten Technology Conference 2015 [2015/11/21]
- Solve Project Euler in Egison [2015/07/02]
- Software Japan Award Ceremony [2015/02/12]
- Egison Presentation at RubyKaigi 2014 [2014/09/21]
- The 3 Exciting Moments Developing Egison [2014/08/26]
- Evolution of Egison Website in This 8 Months [2014/08/21]
- The Ruby Gem for Ultra Super Pattern Matching [2014/06/16]
- The 6 Programming Languages Interesting to Try [2014/05/21]
- Evolution of Programming Languages [2014/05/12]
- My Aim - Thoght on Artificial Intelligence [2014/05/09]