Egisonでゲージ理論 - 量子と古典の物理と幾何@九大
2017年11月19日に九州大学で開催された研究会「量子と古典の物理と幾何@九大」にて,Egisonについて講演させていただきました. 数学とコンピュータⅡ Advent Calendar 2017の1日目の記事として,その講演をスクリプトつきで用意しました.
最新のEgisonは,独自のアイデアにより,テンソルの添字記法や微分形式による微分方程式の表現など微分幾何学で使われている数学の表現をサポートしています. この機能により,ゲージ理論の教科書にのっているような計算を,数式に近い簡潔な記述で表現できます. 本講演では,これらのアイデアとその応用として具体的なプログラムの例を紹介しました.
#1

おはようございます.ご紹介にあずかりました江木です.
本日は,テンソルの添字記法や微分形式による微分方程式の表現など微分幾何学で使われている数学の表現を,プログラム上で表現するために私が開発した手法についてお話します.
#2
私は,2011年,私が東大の理学部情報科学科の修士の学生だったころにEgisonというプログラミング言語を作り始めました.
私はその開発を通して,プログラミング言語の研究をしています.
今回の微分幾何をプログラムで記述するための機能も,このEgisonに実装しました.
#3

本日の講演の目次です.
まず,はじめにEgison独自の機能について紹介します.
つぎに,Egisonの開発の背景にある哲学についてお話します.
最後に,いろいろなプログラムのデモをお見せします.
#4

では,まずEgison独自の機能についてお話します.
#5

このEgisonという言語は,人類が発見しうるアルゴリズム,すべてを簡潔に表現できるプログラミング言語を作りたいという壮大な動機のもとに作っています.
現在は,その一環として,数理物理学の計算を簡潔に表現する言語を作るという挑戦をしています.
#6

Egisonには3つの独自の機能があり,これらがアルゴリズムの簡潔な表現に役立っています.
第一の機能は,幅広いデータ型に対する強力なパターンマッチです.
第二の機能は,そのパターンマッチを利用して作られたユーザーがカスタマイズ可能な数式処理システムです.
第三の機能は,テンソルの添字記法です.
Egisonはテンソルの添字記法をプログラムでもそのまま使うための工夫が施されています.
これにより,微分形式に対する演算までもが,プログラム上でそのまま表現することができます.
#7

まず最初に,パターンマッチについて説明させてください.
この機能は第二の機能を簡単に作るために非常に大切な機能となっています.
#8
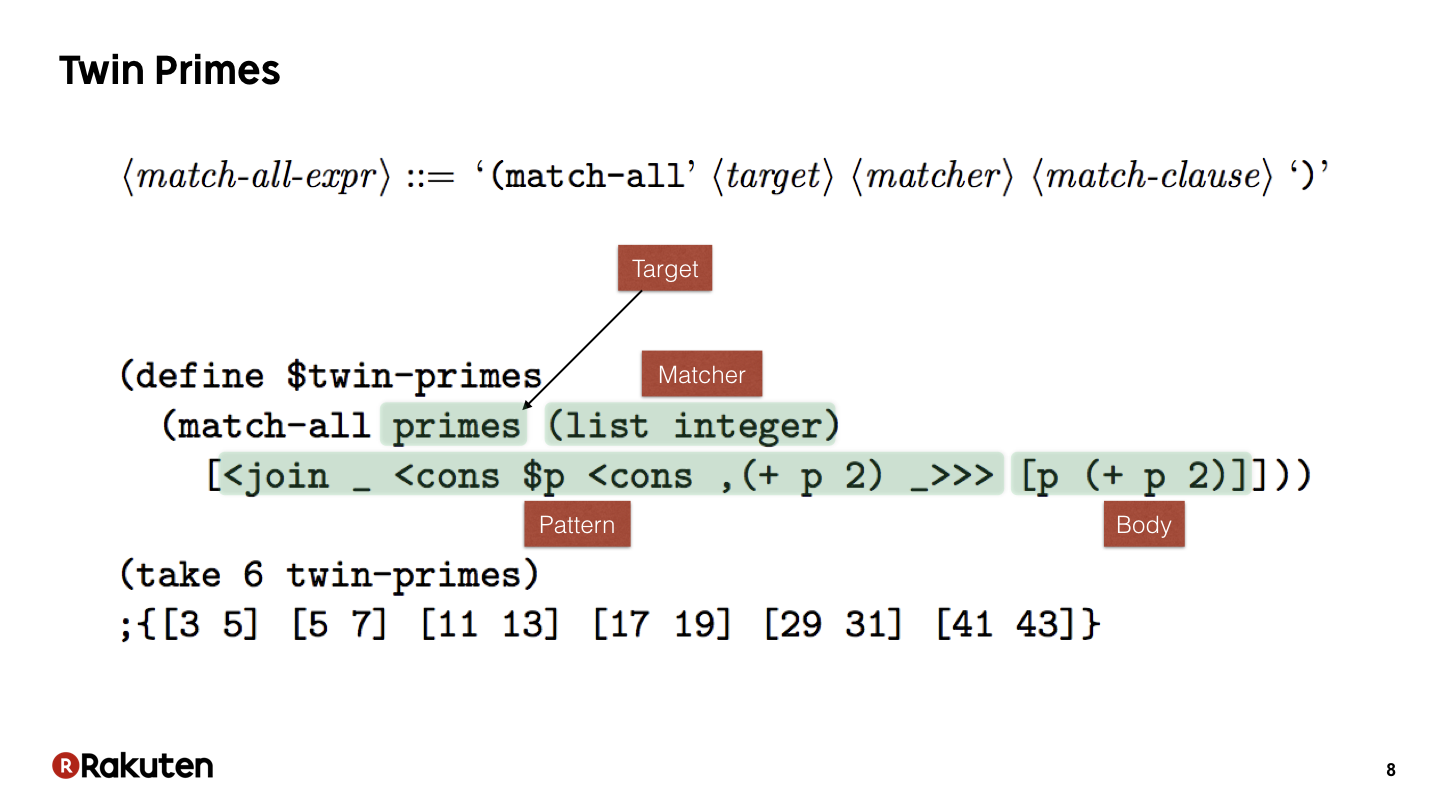
これはEgisonのパターンマッチの例です.
変数primesには素数の無限列が束縛されています.
マッチャーが(list integer)であるのは,このprimesを素数の無限列としてパターンマッチするという意味です.
このパターンは双子素数にマッチするパターンとなっています.
(... パターン部の説明 ...)
そして,pとp+2というタプルを返します.
match-all式は成功したすべてのパターンマッチの結果をコレクションにして返します.
そのため,変数twin-primesには,すべての双子素数からなるコレクションが束縛されます.
プログラム(take 6 twin-primes)の部分で,先頭6つの双子素数を取り出しています.
このようなパターンマッチをサポートしていない言語では,同じことをするプログラムを書くには,ループを使用したプログラムを記述することになり,記述が煩雑になります.
Egisonのパターンマッチを使えば,他のプログラミング言語では,煩雑になるプログラムが簡潔に書けます.
#9
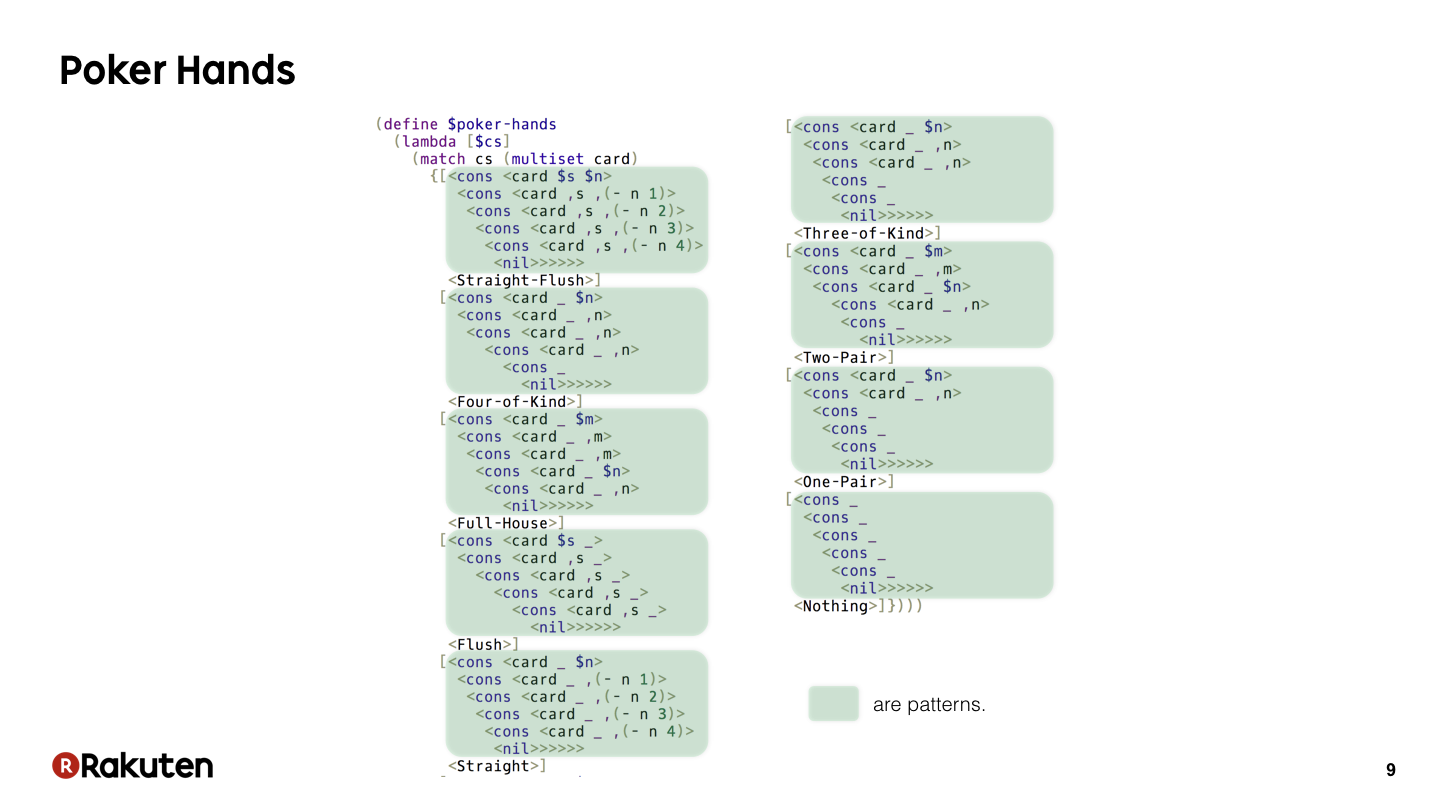
先程のプログラムをコレクションをリストとしてパターンマッチしました.
しかし,Egisonではコレクションを多重集合としてパターンマッチすることもできます.
このプログラムは,それを利用してポーカーの役判定をするプログラムを簡潔に記述しています.
#10

この部分はストレートフラッシュにマッチするパターンです.
#11
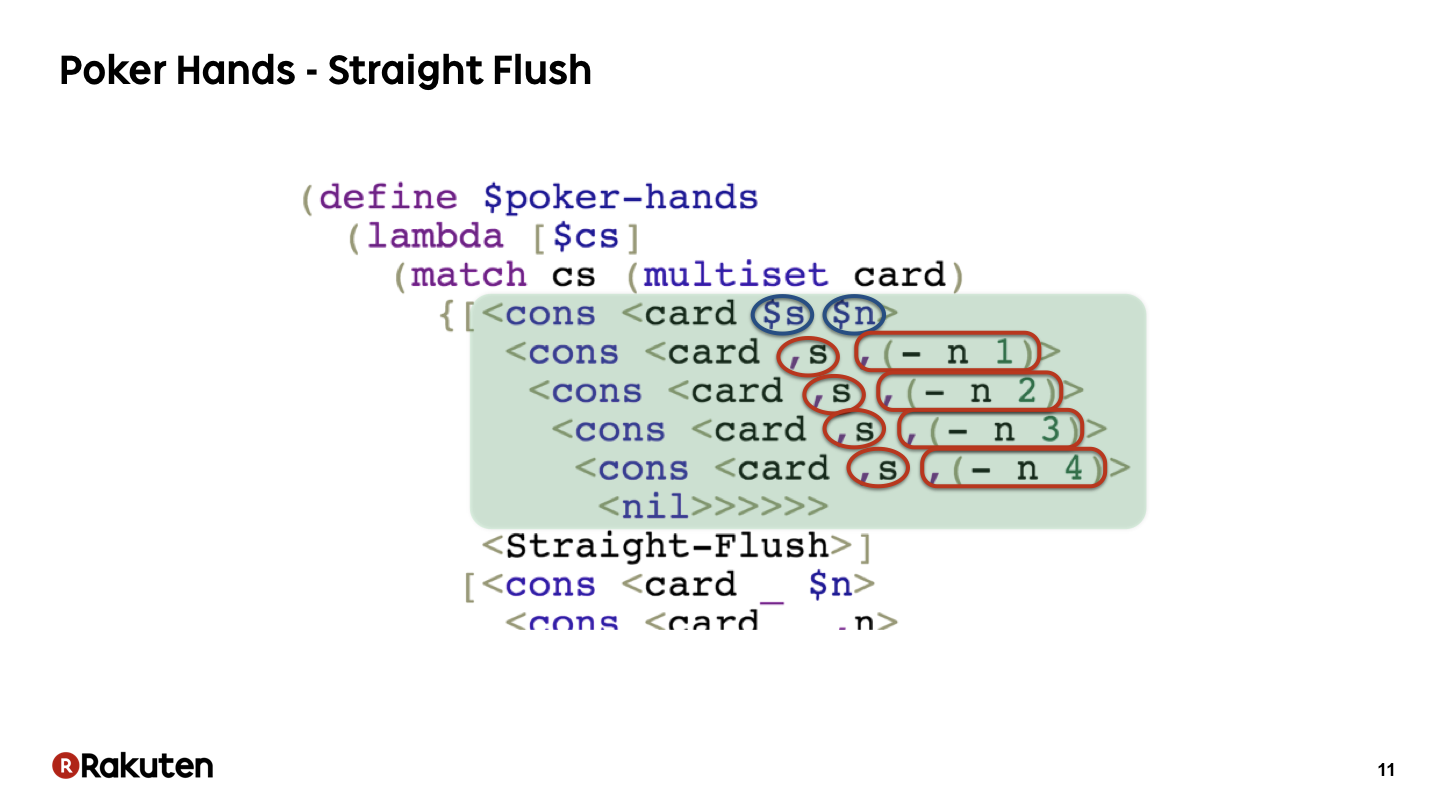
このように非線形パターン(パターン変数に束縛された値を同じパターン内で参照するようなパターン)を利用して,ストレートフラッシュにマッチするパターンを記述しています.
#12
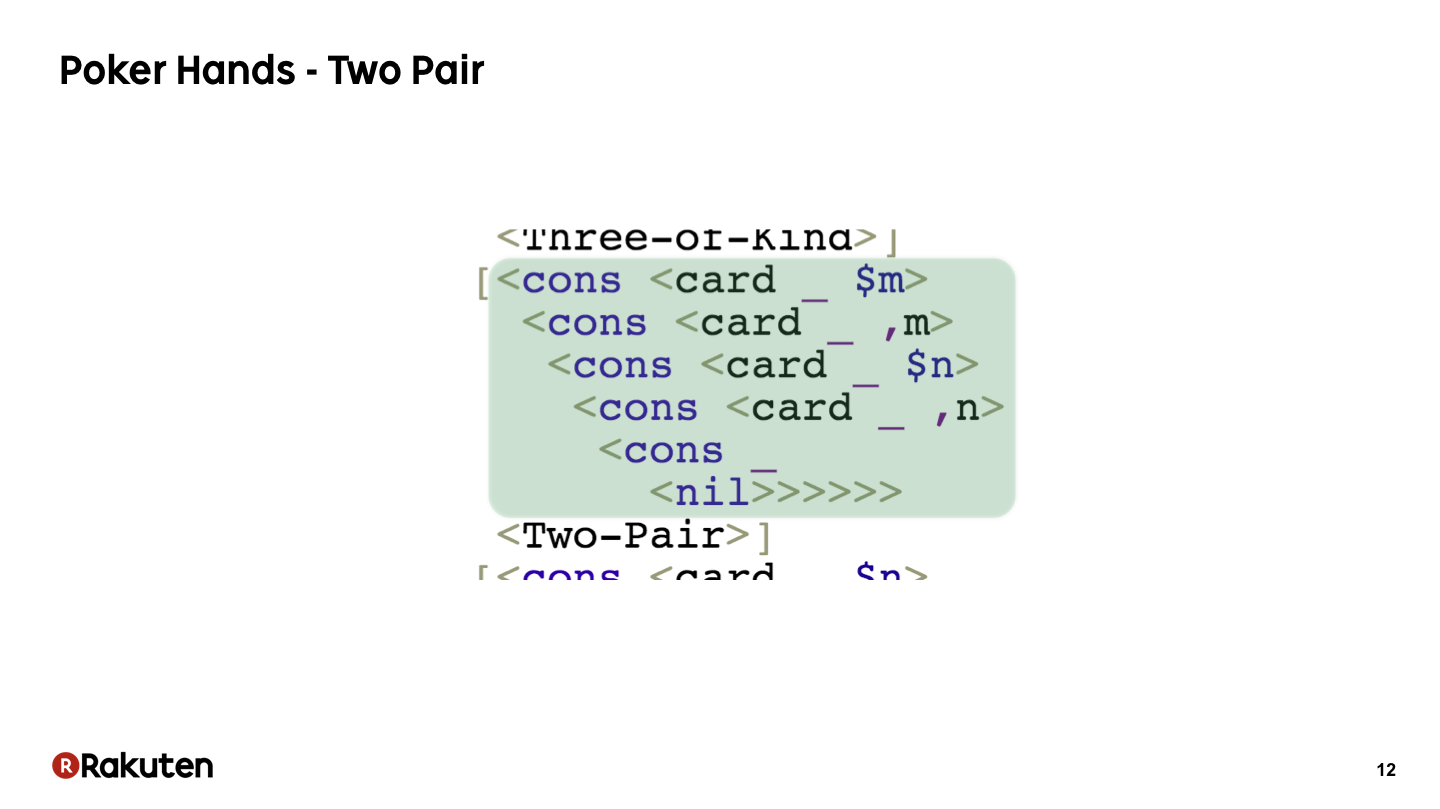
これはツーペアのパターンです.
#13
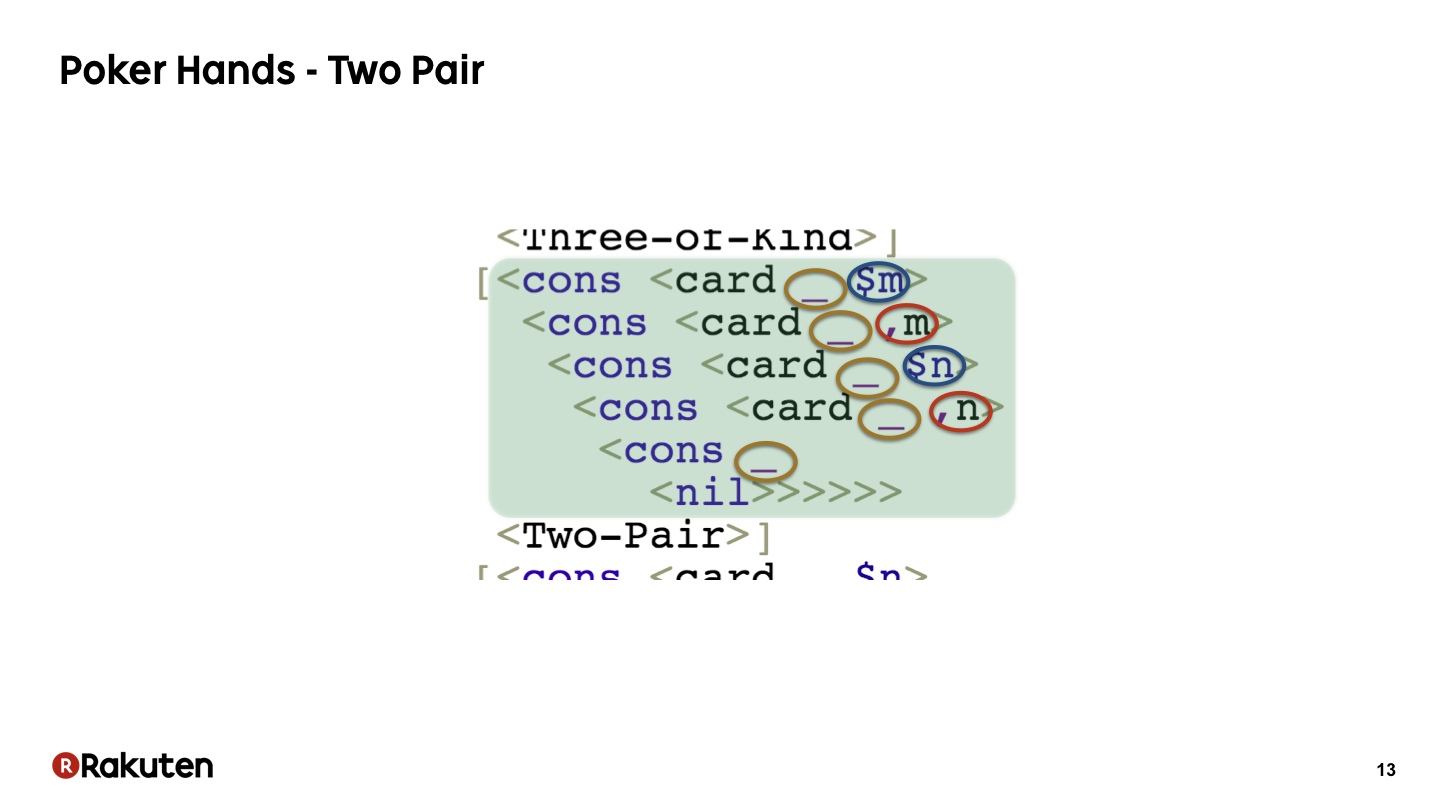
先程の例と同様,_はワイルドカードを表しています.
#14

先程紹介したlistやmultisetというマッチャーは,言語決め打ちのものではなく,ユーザー自身がEgisonを使って定義できるようになっています.
これはmultisetマッチャーの定義の例です.
#15

multisetのconsパターンの定義の例をお見せしてその定義方法を説明します.
#16

consパターンコンストラクタは2つのパターンを引数にとり,それぞれのパターンは,要素のマッチャーaと(multiset a)として再帰的にパターンマッチされ,ターゲットは,ターゲットが{1 2 3}というコレクションだった場合,1と{2 3},2と{1 3},3と{1 2}という3通りの分解のされ方があるということを定義しています.
このようなユーザによるデータ型ごとのパターンマッチの方法の定義にもとづいて,言語処理系により比較的シンプルなアルゴリズムによってパターンマッチは実行されます.
この機構の設計がEgisonのパターンマッチを作る上で挑戦的な問題でした.
#17

Egison以前のプログラミング言語では,consやjoinはリストに対してのみ定義されているものでした.
#18

Egisonでは,これらのパターンコンストラクタをmultisetやsetに対しても意味がもつように意味を拡張しました. このようなパターンコンストラクタの多相性を導入したのもEgisonの貢献の1つです.
#19

次は,このパターンマッチを利用して作られた数式処理システムについて説明します.
#20

これはシンボリックな計算の例です.
シンボリックな計算をサポートしている言語では,xやy,iなどといった変数をそのまま数のように扱えます.
#21

Egisonはパターンマッチにより,cos(θ)^2 + sin(θ)^2 = 1やω + ω^2 = -1のような簡約規則をユーザーが定義できるようになっています.
可換なかけ算とたし算からなる数式は項の多重集合とみることができ,項は因子の多重集合と考えることができます.
そのため,Egisonのパターンマッチを使うとその簡約規則を簡単に記述できます.
#22

これは,ガロア理論のアイデアを利用して,1の7乗根の冪根による表示を求めるプログラムです.
1の3乗根がうまく簡約されているおかげで,きれいに答えが求まっています.
EgisonのWebサイトには,他にもいくつかの代数方程式を解くプログラムを掲載しています.
#23

これは偏微分演算子をしている例です.
先程のお話した簡約化のプログラムと同様にパターンマッチを使って簡単に定義しています.
これだけの定義で,微分幾何ででてくるような関数については微分することができます.
#24

微分演算子は,実際にこのように使うことができます.
#25

テイラー展開をするプログラムもこのように実装できます.
多変数テイラー展開も実装できます.
#26

テイラー展開の実行例です.
#27

次にテンソルの添字記法をプログラミングに導入する手法について説明します.
この手法は,今まで説明してきたパターンマッチの機構とは独立したものとなっています.
#28

これはリーマン曲率テンソルの公式です.
テンソルの添字記法を使った数式では,テンソルに添字がたくさん付加されます.
この公式をEgisonはそのまま表現できます.
#29

これはEgisonによるプログラムをWolfram言語(Mathematica)と比較したものです.
Wolfram言語では,微分演算子Dを直接テンソルに適用できないため,Table構文を用いて配列Γとxの要素にアクセスし,その結果に対して微分演算子Dを適用する必要があります.
そのため,プログラムの記述が数式やEgisonによるプログラムに対して,煩雑になります.
またアインシュタインの縮約規則もサポートできていないため,Sum式を明示的に書く必要もあります.
Egisonでは,偏微分演算子∂/∂もテンソルのかけ算.の両方ともテンソルに対して適用できます.
そのため,数式をそのままプログラムに翻訳できます.
#30

Egisonでさきほどの例のように数式をそのままプログラムに翻訳できるようになったのは,関数をここで述べるようなスカラー関数とテンソル関数という2種類の関数に分類し,区別したからです.
スカラー関数は,たし算やかけ算,偏微分のようなスカラーに対して定義された関数です.
これらの関数はテンソルが適用された際に,自動で要素ごとにマップしたい関数です.
対して,テンソル関数は,テンソル同士のかけ算や,行列式の計算をするような関数のことです.
これらのテンソルに対して定義される関数は,要素ごとに自動でマップすると問題があります.
テンソル関数の場合は,引数がテンソルだった場合は,テンソルをテンソルとしてそのまま扱います.
スカラー関数とテンソル関数という2種類の関数に関数を分類し,区別して扱うとテンソルの添字記法をプログラムでもそのまま使えるという発見が今回の研究の新規性です.
#31

実際にはスカラー仮引数とテンソル仮引数という2種類の仮引数の概念をプログラミング言語に導入することにより,スカラー関数とテンソル関数の区別を実現しました.
仮引数の先頭に$が付加されているとそれはスカラー仮引数です.
対して,仮引数の先頭に%が付加されているとテンソル仮引数になります.
仮引数がスカラー仮引数の関数に,テンソルが適用されると,関数の処理はテンソルの要素ごとに自動でマップされます.
それに対して,仮引数がテンソル仮引数の関数に,テンソルが適用されると,仮引数はテンソルそのものに束縛されます.
#32

これはスカラー関数として定義されたmin関数をベクトルに対して適用している例です.
min関数は2つの整数を引数にとり小さい方の数を返す関数です.
このように自動でテンソルの要素ごとに処理がマップされます.
そのおかげでスカラー値に対してしかmin関数は定義されていなくても,テンソルに対してmin関数を適用することができます.
#33

これは,テンソル関数の例として,テンソル同士のかけ算のための.関数を定義した例です.
contractは,上下で同じ添字がある場合,その対角成分について第1引数で指定された関数で畳み込む組み込み関数です.
この.関数で,あらゆるテンソルのかけ算を表現できます.
#34

スカラー関数の実装は非常に簡単です.
スカラー仮引数があった場合,それをテンソル仮引数に変換し,tensor-map関数を挿入するだけです.
#35

実際にリーマン幾何学にあらわれる計算をEgisonで記述してみます.
#36

これは球面の曲がり具合を表現するリーマン曲率テンソルを計算するプログラムです.
#37

この部分では球座標の設定をし,その局所基底を計算しています.
#38

ここでは球面のリーマン計量を計算しています.
このように,g__とg~~それぞれに違う行列を束縛することができます.
#39

これは第一種クリストッフェル記号を計算している箇所です.
#40

これは第二種クリストッフェル記号を計算している箇所です.
#41

これはリーマン曲率テンソルを計算している箇所です.
#42

Ricci曲率やスカラー曲率も同様に計算できます.
#43

計量の部分をこのようにシュヴァルツシルト計量にかえると,原点を中心とした星のまわりの時空間の曲がり具合,重力場の計算ができます.
実は,この計算をするプログラムを,必要あればEgisonを拡張しながら,できるだけ簡潔に記述するという試みをしているうちに,この添字記法の研究はいつのまにか意図せずに完成していました.
#44

ここまで説明したテンソルの添字記法をプログラミングに導入する手法については今年の9月にICFPに併設して開催されたSchemeワークショップにて論文を発表しました.
#45

ここまで説明してきたテンソルの添字記法をプログラミングに導入する手法を少し拡張すると微分形式もプログラムで自然に表現できることを最近発見しました.
ここから,これについて説明します.
#46

数式では,n階のテンソルにk個の添字が付加されている場合,そのテンソルを(n-k)形式として解釈します.
例えば,3階のテンソルにω~i_jと2つ添字が付加されていた場合は,そのテンソルを1形式として扱います.
#47

そこで,プログラムでも,添字が省略された場合に,テンソルは微分形式として解釈されることにします.
ここで,添字が省略された場合の添字の補完の規則をうまく設計することにより,プログラムでも微分形式を自然に表現できるということを最近発見しました.
例えば,A,Bはスカラーを値に持つ2形式とします.
デフォルトでは,上の例のように,省略された添字については,同じ組み合わせの添字を自動的に補完します.
ただし,ウェッジ積のような微分形式のための特別な演算の場合には,このような補完では適していないことがあります.
例えば,ウェッジ積の場合は,下の例のように,引数のそれぞれに全て異なる添字を補完したいです.
そのような補完をしたいときのために!という構文要素を追加しました.
!が関数適用の前に付加されている場合は,引数のそれぞれに全て異なる添字を補完します.
#48

そのため,一般ユーザーは!について意識する必要はない.
このように,テンソルの添字が省略された場合の,添字の補完方法を制御するための構文を導入することにより,微分形式の計算は表現できる
#49

ウェッジ積はこのように実装できます.
#50

これは外微分を実装しています.
#51

ホッジ作用素も実装できます.
このサンプルでは,nlabにのっているこの数式をプログラムで表現することにより,ホッジ作用素を定義しています.
ユークリッド空間の計量におけるホッジ作用素が定義されています.
#52

これはMinkowski空間における計量についてホッジ作用素を定義したものです.
#53

ホッジ作用素と外微分作用素を組み合わせると余微分作用素も簡単に定義できます.
#54

ここから,もうすこし応用的な微分形式の計算をするプログラムの例をお見せします.
#55

これはホッジラプラシアンを定義しているサンプルです.
ラプラシアンはデカルト座標ではシンプルな形をしていますが,例えば極座標や球座標など一般の座標系では複雑な形になります.
微分形式のための演算子dとδがあれば,リーマン計量を設定するだけで,一般の座標系についてラプラシアンを自動で計算することができます.
#56

これは,Euler類という特性類についての計算です.
球面のEuler形式という微分形式を求めています.
#57

Euler形式を計算する場合は,接続形式が対称である必要があります.
この公式のように基底を変換することで接続形式を対称にしています.
Euler形式を球面全体で積分すると,2となります.
これは球面のEuler数と同じです.
トーラスについて同じことをすると,トーラスのEuler数0が求まります.
#58

これはU(1)ゲージ理論の計算をEgisonでしている例です.
dF=0,δF=0が,電荷のない空間のマクスウェル方程式と同値であることを確かめています.
#59

ここまで紹介したEgisonのプログラムは,Egison Math Notebookという形で公開されています.
#60

この研究の応用先として,スパコンで高速に動く物理シミュレーションエンジンとつなげることを考えています.
例えば,Formuraは,偏微分方程式に近いかたちのプログラムをスパコンで動くコードに変換するコンパイラです.
Egisonを使えば,微分形式の言葉で記述した微分方程式を,偏微分方程式に変換できます.
FormuraにEgisonをつなげると,微分形式の言葉で書かれた微分方程式をスパコンで高速に実行できうるようになります.
またHaskellで流体シミュレーションエンジンを開発されている九州大学の深川さんとも共同研究を進めています.
#61

ここから,Egisonを作った背後の哲学について語らせてください.
#62

最初に述べたとおり,人間が発見しうるすべてのアルゴリズムを簡潔に表現できる言語を作りたいというモチベーションでEgisonは作られています.
#63
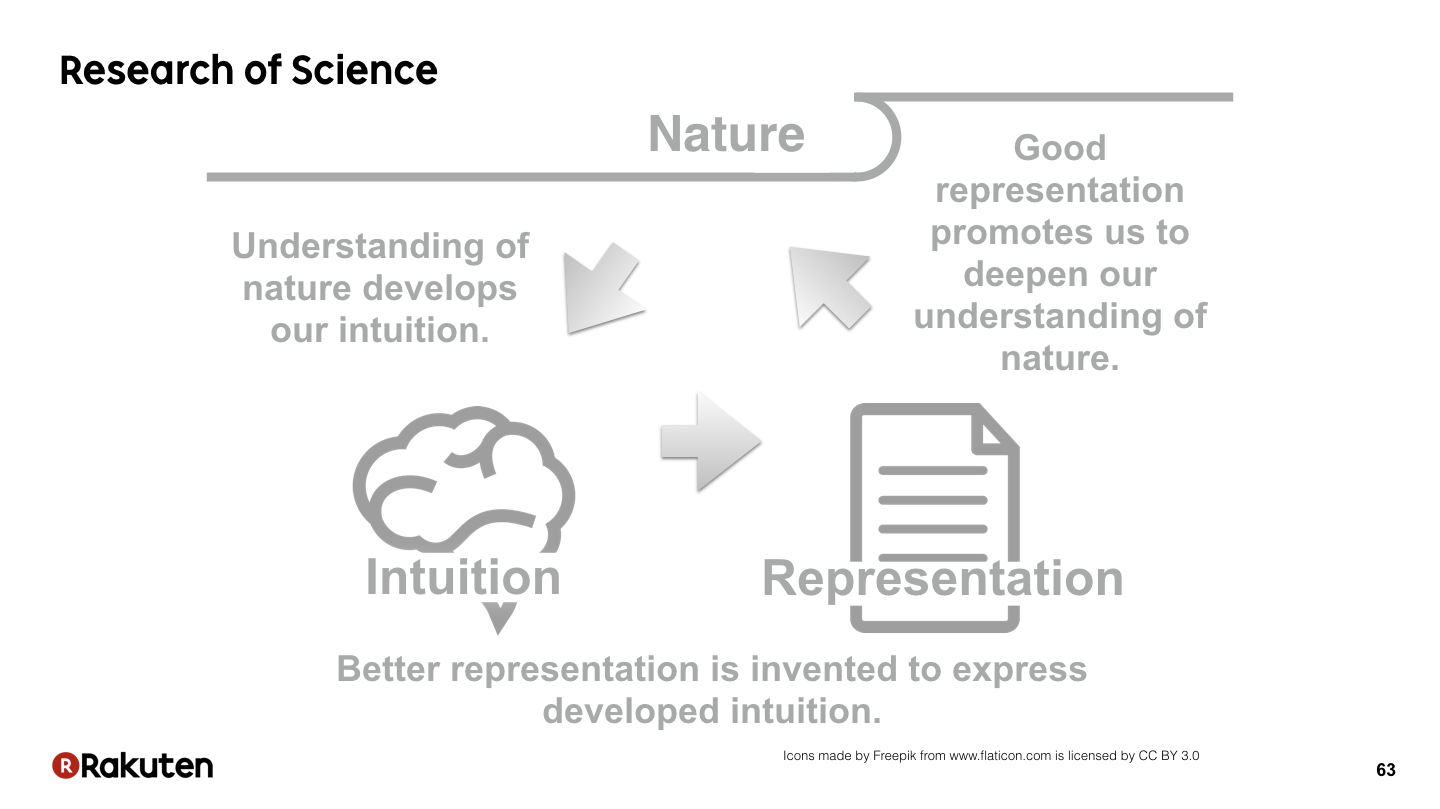
これまた,壮大なスライドですが,これは科学の研究について図示したものです.
自然を観察することによって我々の直感は深まります.その結果,我々が使っている表現と我々の直感の間にギャップが生じます.
そして,そのギャップを埋める新しい表現が発明されます.
その新しい表現を通して自然を観察すると,より深い自然の理解が得られます.
その結果,我々の直感はさらに深まります.
科学の研究は,このようなループであり,そのため表現の研究はとても重要であるということをこのスライドはいっています.
また,このような事を考えにもとづくと,自然を深く理解することが言語の研究のために必要だという考えてにいたり,数学や物理を勉強し,その専門的な計算を表現することに注力するようになりました.
#64
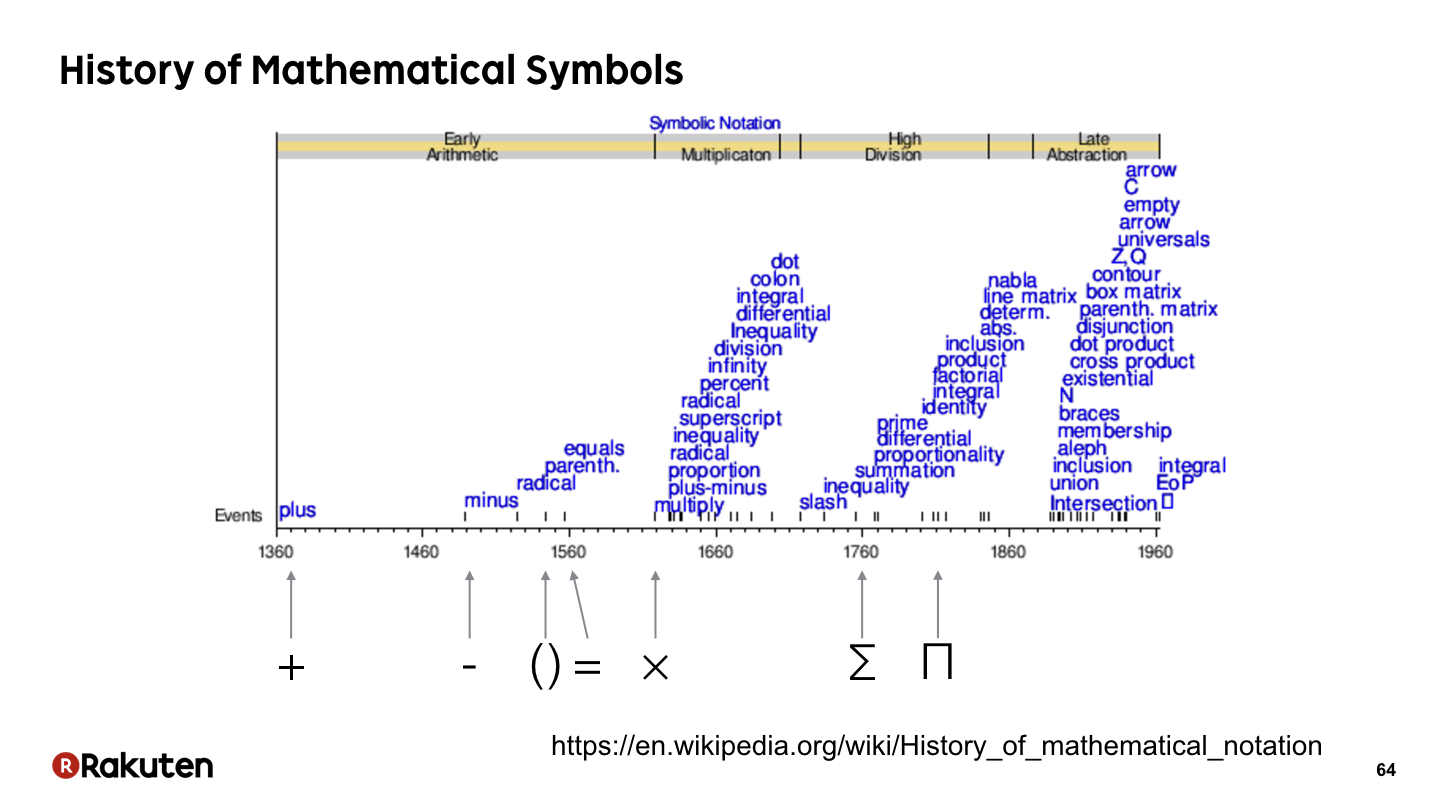
例えば,数学のシンボルの歴史にもこのループを見ることができます.
#65

また,直感と表現のギャップを感じるのにもっとも手っ取り早い方法は,数の表記をくらべることです.
それぞれの文明の数の表記は,まったく扱いやすさが違います.
プログラミング言語によるアルゴリズムの表現は,この数の表記を複雑にしたものと考えることができます.
#66
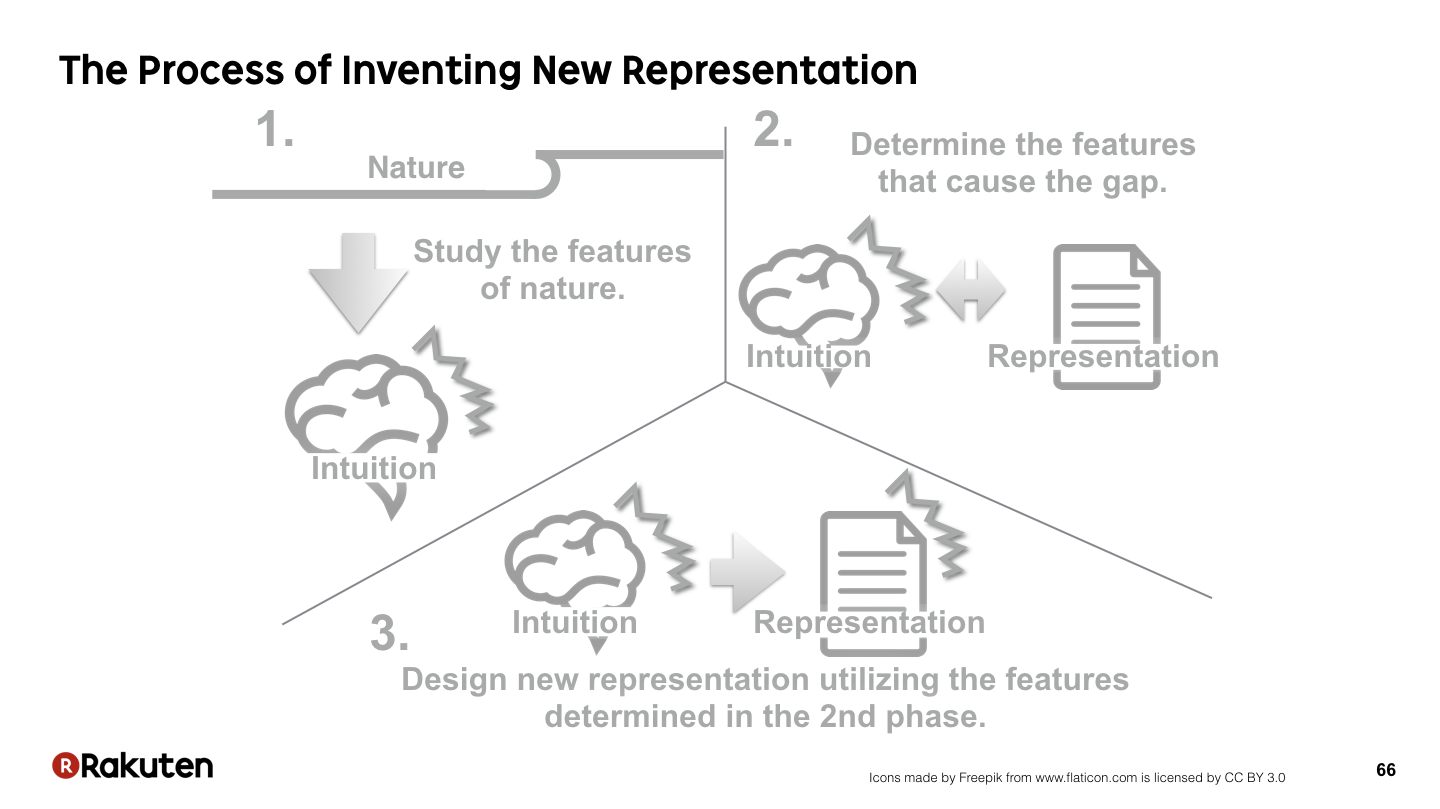
このスライドは,新しい表現を発明するプロセスについてまとめたものです.
#67
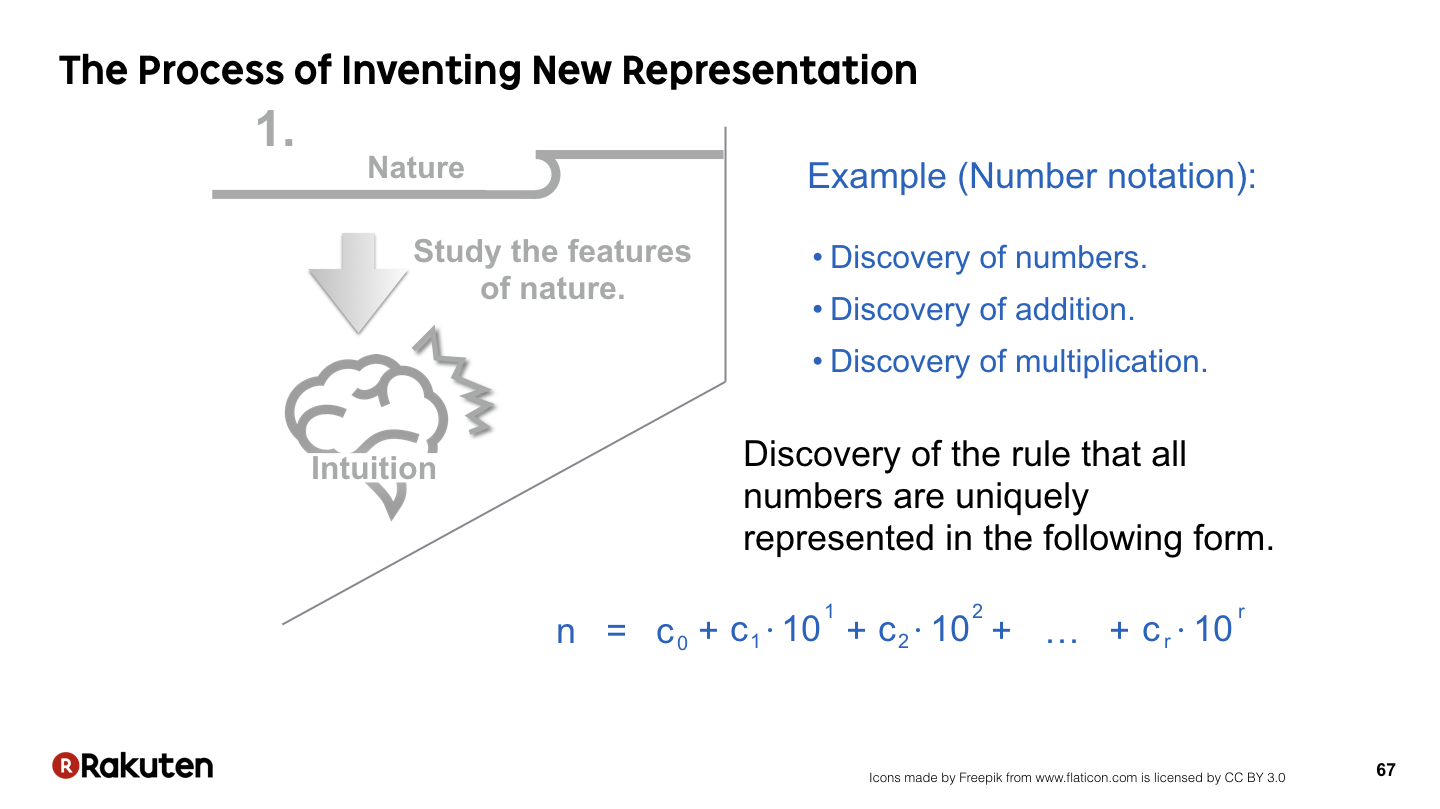
最初に自然を観察します.
数の場合,数の概念の発見や,たし算・かけ算の発見,このような形で数が一意的に表せるという感覚などを養うことが,数の表記法を発明するためには重要です.
#68
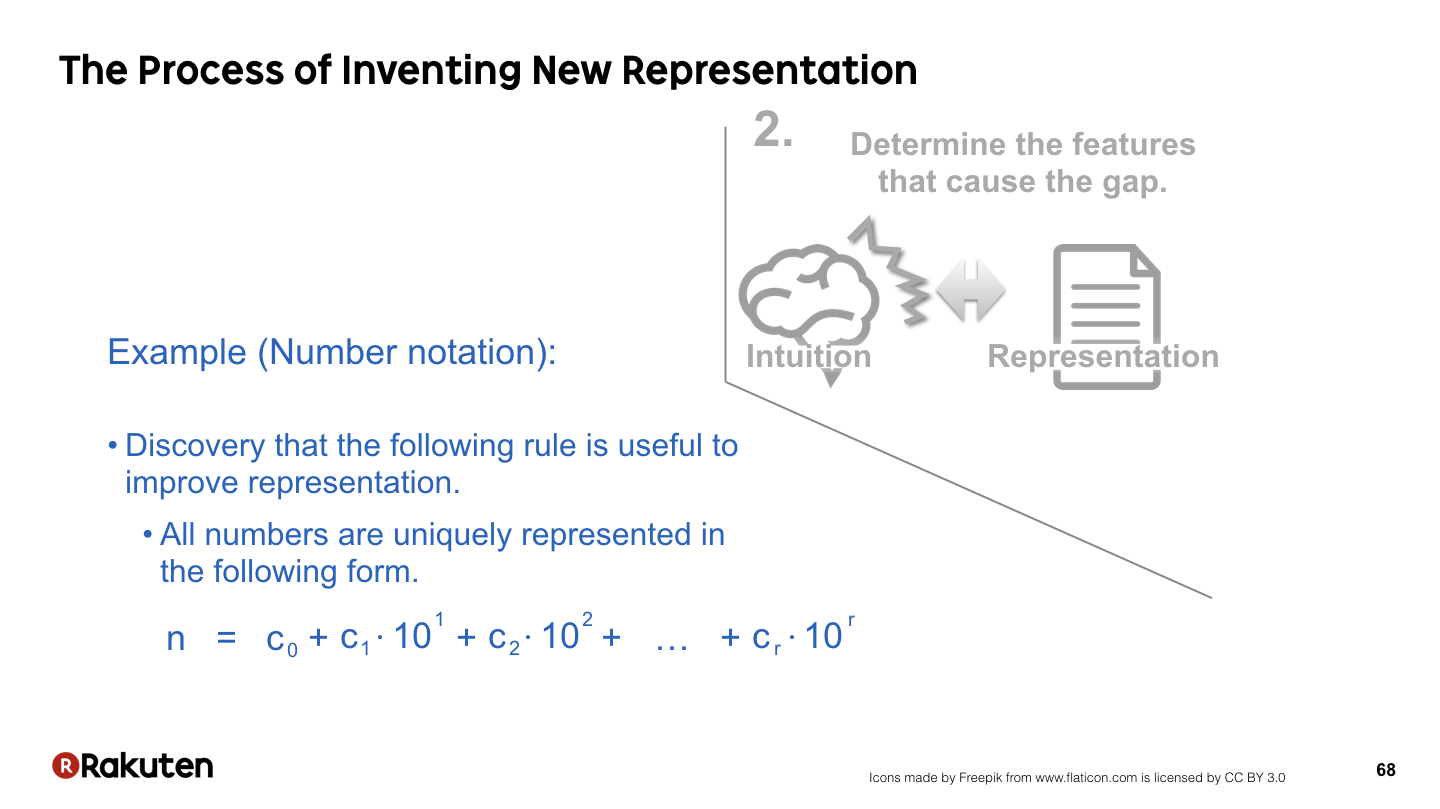
数に対する理解が深まると,ただ棒を並べて数を表現する表記と直感との間に大きなギャップが生じます.
そのギャップの原因を分析することにより,より良い数の表記に役に立つ数の法則が何なのかわかってきます.
#69
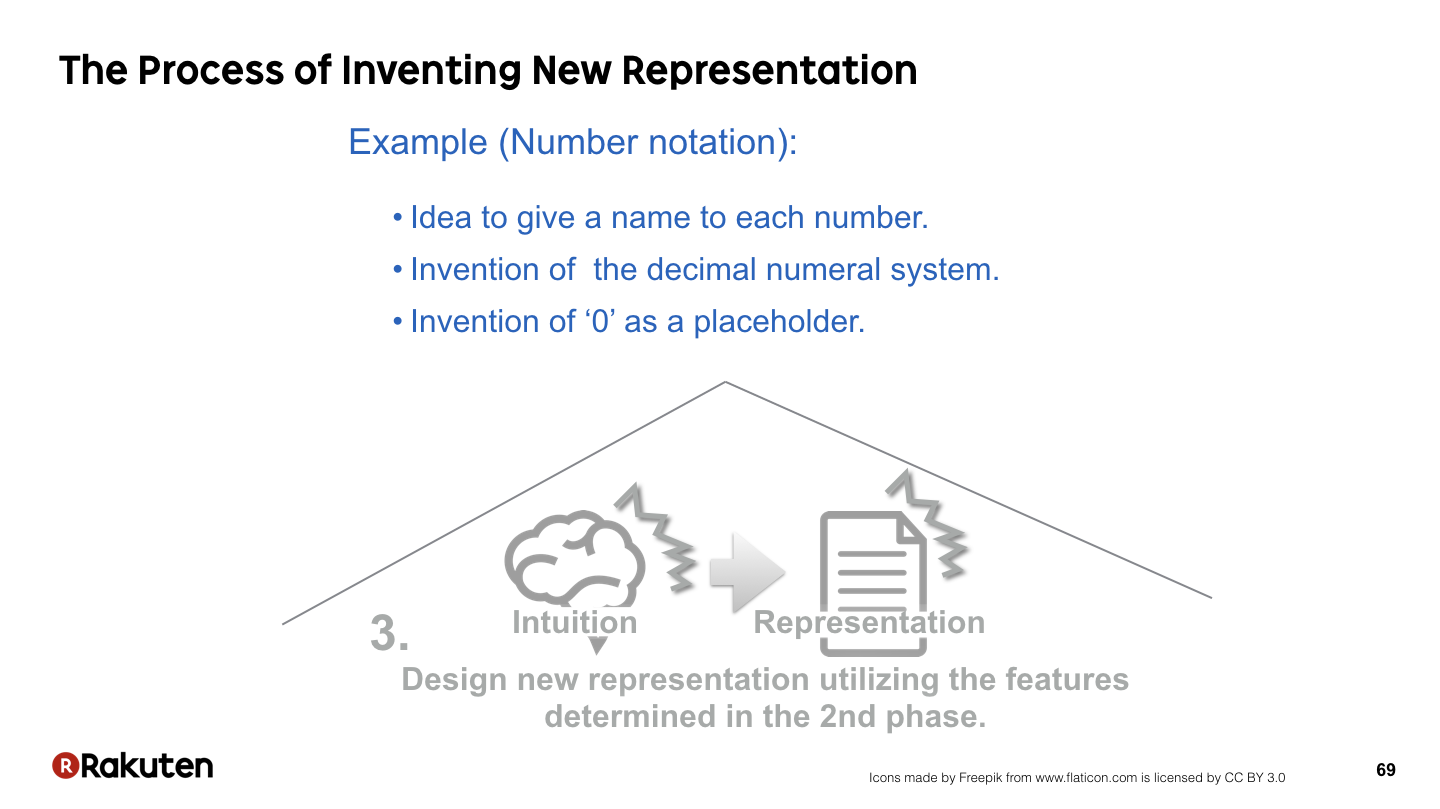
その結果わかった数の法則を活かして,表記のデザインをします.
このフェーズでは,それぞれの数に名前を与えるというアイデアや,複数の数を並べることにより1つの数を表現するアイデア,10進数のアイデア,0をプレースホルダーとして使うアイデアなどのようなデザイン上のアイデアを得る必要があります.
#70
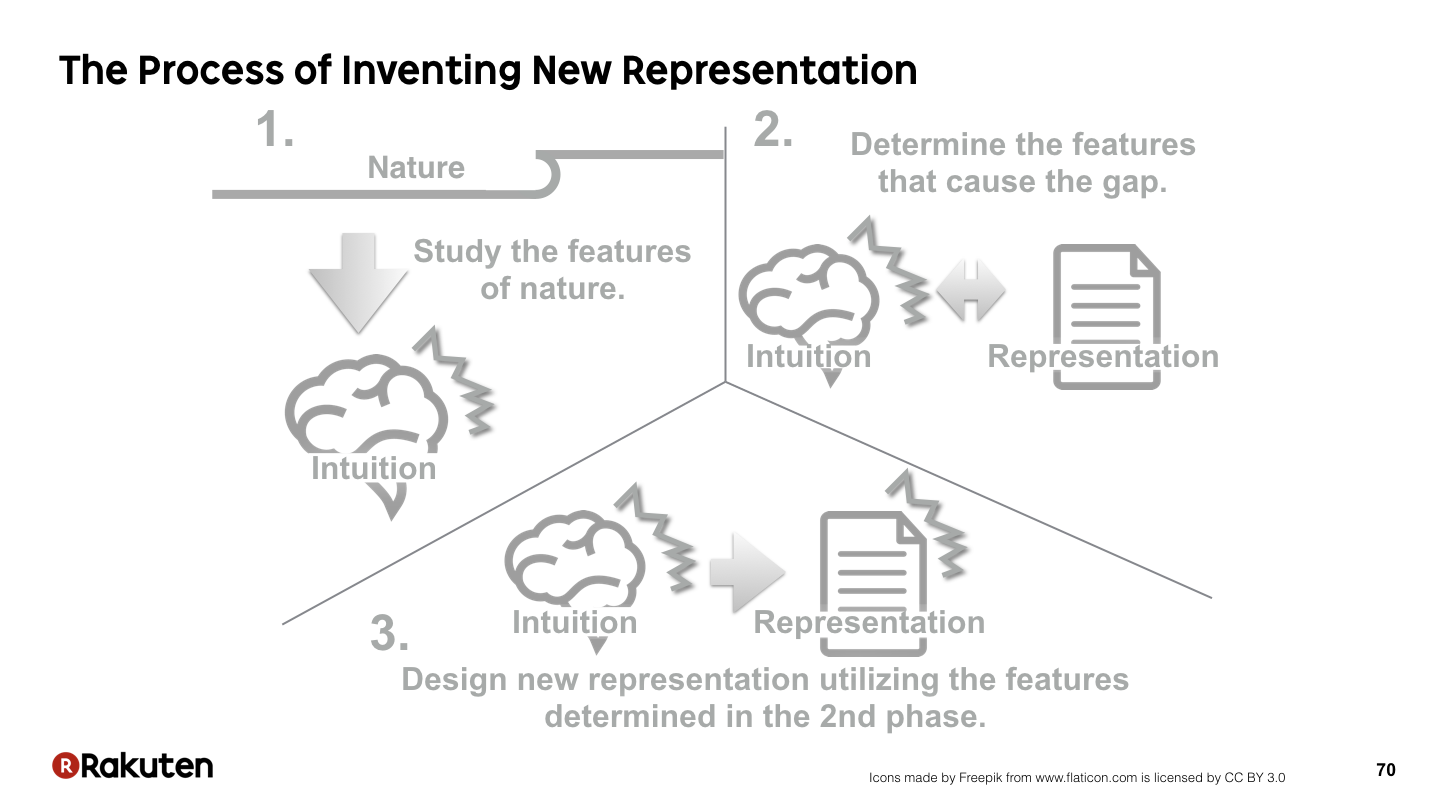
まだ定式的な説明にはなっていませんが,大体このようなプロセスを経て,新しい表現は発明されるというようなことを考えています.
#71

人間にとって表現とは何かという問題を深く考えることは,非常に重要だと考えています.
先程のべた「新しい表現方法をみつける一般的な方法はあるか?」という問題の他にも,「プログラミング言語の表現力を定式的に測る方法はあるか?」など重要な問題はいくつもあります.
これらの答えが見えたとき,人類にとって全く新しい世界観が得られると考えています.
この講演でお話したプログラミング言語の研究をする際にも,このような大きな問題も念頭において研究しています.
#72

では,最後に実際にいくつかデモを動かしてみます.
(... 略 ...)
#73

ありがとうございました.