第10回日本OSS奨励賞受賞LT

この度、Egisonについて日本OSS奨励賞という国内で有名な賞を頂けることになりました。 その受賞LTのために作成したプレゼンテーションを公開します。

#1

こんばんは。ご紹介に与りました江木です。 本日は「プログラミング言語Egisonと表記法の進化について」というタイトルでお話します。

#2

本日のお話は、Egisonの簡単な紹介をしたあと、表記法を進化させるということについて手短に説明するという流れになっています。

#3

ではEgisonについて簡単に紹介します。

#4

Egisonはパターンマッチ指向という新しいパラダイムを掲げているオープンソースのプログラミング言語です。 継続的にリリースを重ねており、最初のリリースからは4年以上経っています。

#5

Egisonの特徴は、非自由データと呼ばれる1つの定まった標準形を持たないデータに対しても柔軟なパターンマッチが表現できるところにあります。 非自由データの例としては、要素の重複は考慮するが、順番を考慮しないコレクション型である多重集合などがあります。

既存の言語では多重集合を扱う際、コレクションを多重集合として直接パターンマッチできないため、これをリストとして扱い、何重にもネストしたループや条件分岐を記述せねばならないことがあります。 そのような場面でも、Egisonでは多重集合に対するパターンマッチが記述できるため、このようなシンプルなパターンマッチ式で同じことができます。

#6

Egisonのわかりやすい応用として４つの例をお見せします。

#7

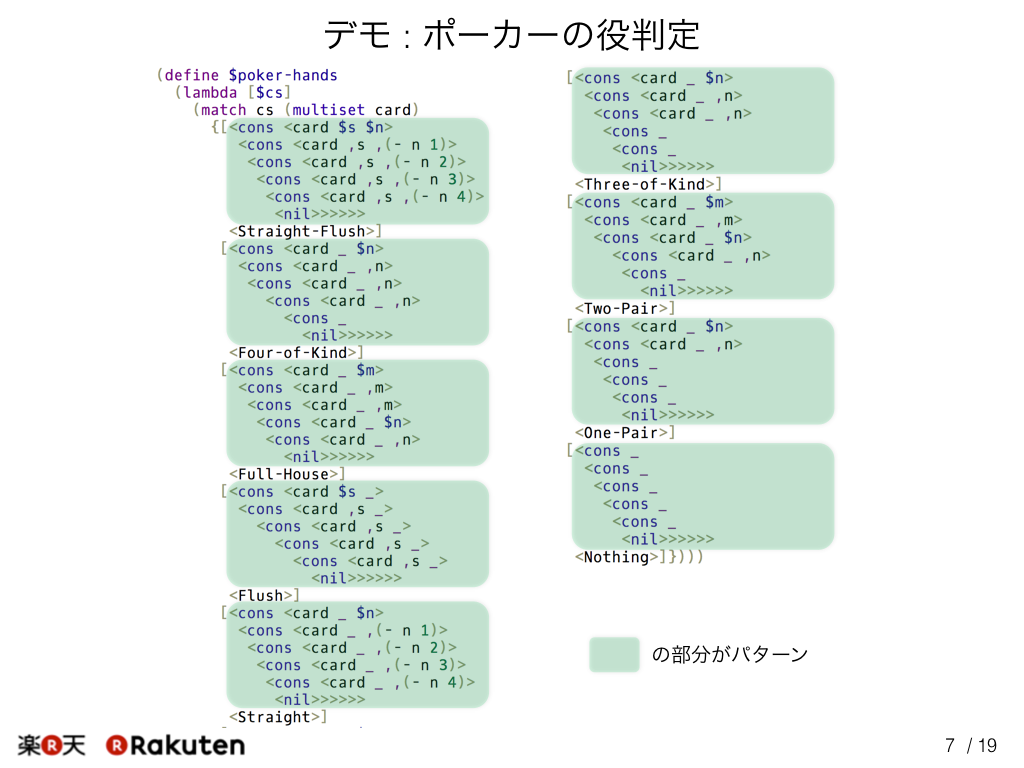
最初のEgisonのデモとして、ポーカーの役判定プログラムをよくデモしています。 カードの並びの順番を考慮しない多重集合としてパターンマッチすることにより、すべての役についてそれぞれ1つのパターンで書くことができます。

#8

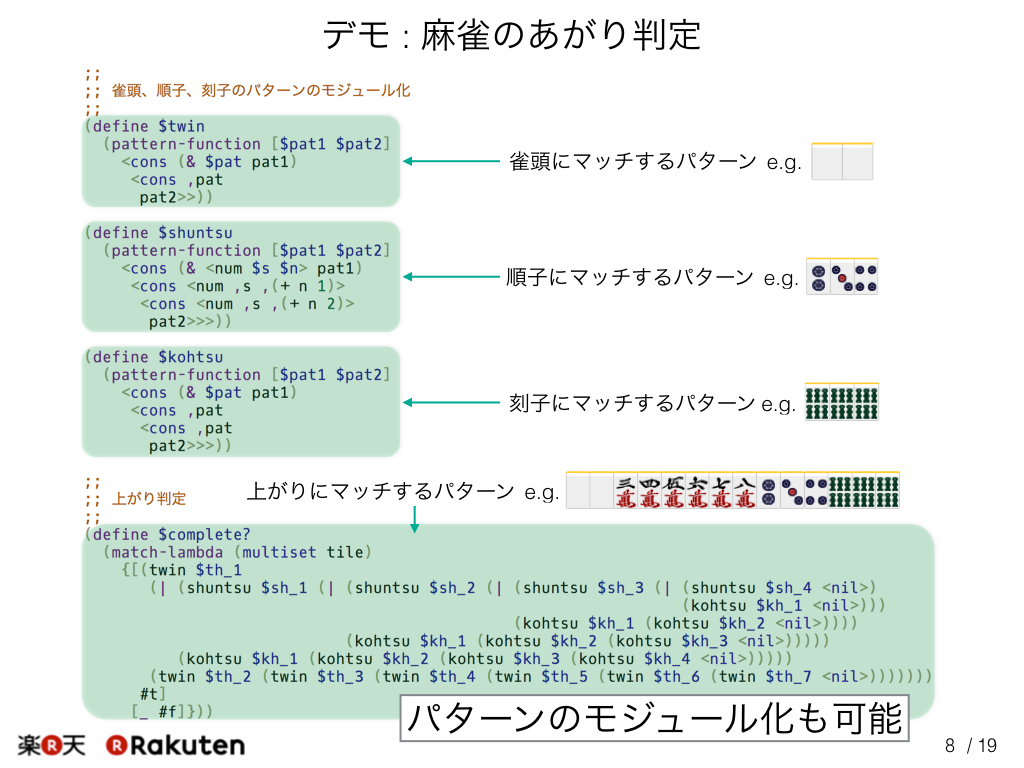
また、麻雀の上がり判定を1枚のスライドに収まるプログラムで記述することもできます。 このように2つの同じ牌からなる雀頭、3つの連番の牌からなる順子、3つの同じ牌からなる刻子にマッチするパターンをモジュール化できます。 Egison以外の言語で同じことを書くと、読むだけでも大変なプログラムになってしまいます。

#9

これは素数の無限列から双子素数の組を列挙するパターンマッチとなっています。 Egisonは、複数の結果を持つパターンマッチにも対応しています。 それにより、このパターンマッチ式により任意の個数の双子素数を列挙することができます。

#10

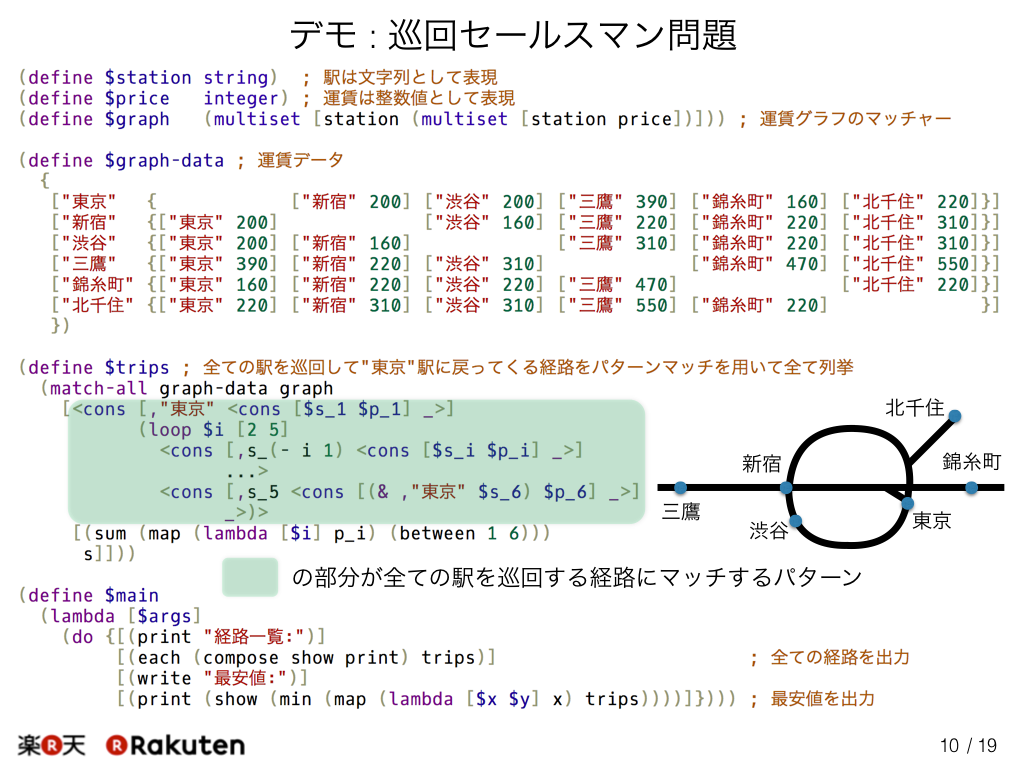
これはグラフのパターンマッチの例です。 このプログラムは巡回セールスマン問題を解くプログラムです。 東京駅から出発し、ここにあげた東京の5つの駅すべてを訪ね東京駅に戻ってくる経路のうち、運賃が最安値の経路を見つけるプログラムになっています。

この緑の部分のパターンにより、全ての駅を巡回する経路を列挙しています。 この部分を編集するだけで、色々な種類の経路を列挙することができます。

#11

では、次に表記法の進化についてお話します。

#12

人間の直感による認識をより直接的に表現するように表記法は進化してきました。 我々のよく知る表記の進化には、数の表記の進化とプログラムの表記の進化があります。

#13

新しい表記法はこのような手続きを繰り返すことにより、発明されます。 次以降のスライドで自然数の表記の進化の歴史を具体例にこのことを見てみます。

#14

最初のフェーズでは数についての数学的法則が研究されます。 より簡潔な数の表記のためには、まず、数についての数学的法則の発見が必要です。 というのはより簡潔な数の表記の設計や読解には、数についての数学的性質を使うからです。 例えば、ローマ数字を読むのに掛け算の概念は必要ないですが、10進表記の数を理解するには掛け算の概念が必要です。

#15

また、多くの数学的法則を発見し、知ることにより、我々の数学的直感は初めて成長します。 そうすると、それまでに使っていた表記と、我々の直感による認識に隔たりが生じるようになります。

#16

その隔たりの原因を分析することにより、表記に役立つ数学的法則を選出、または新たに発見することができます。 この分析に成功すると新しい表記のアイデアが生まれます。

そして、最後にそれらの数学的法則を応用して新しい表記法をデザインします。 この表記法のデザインも非常に難しいフェーズです。 表記に関する数の性質とは独立した工夫や、この段階で初めて必要になる新たな数学的法則の発見が必要であったりします。

#17

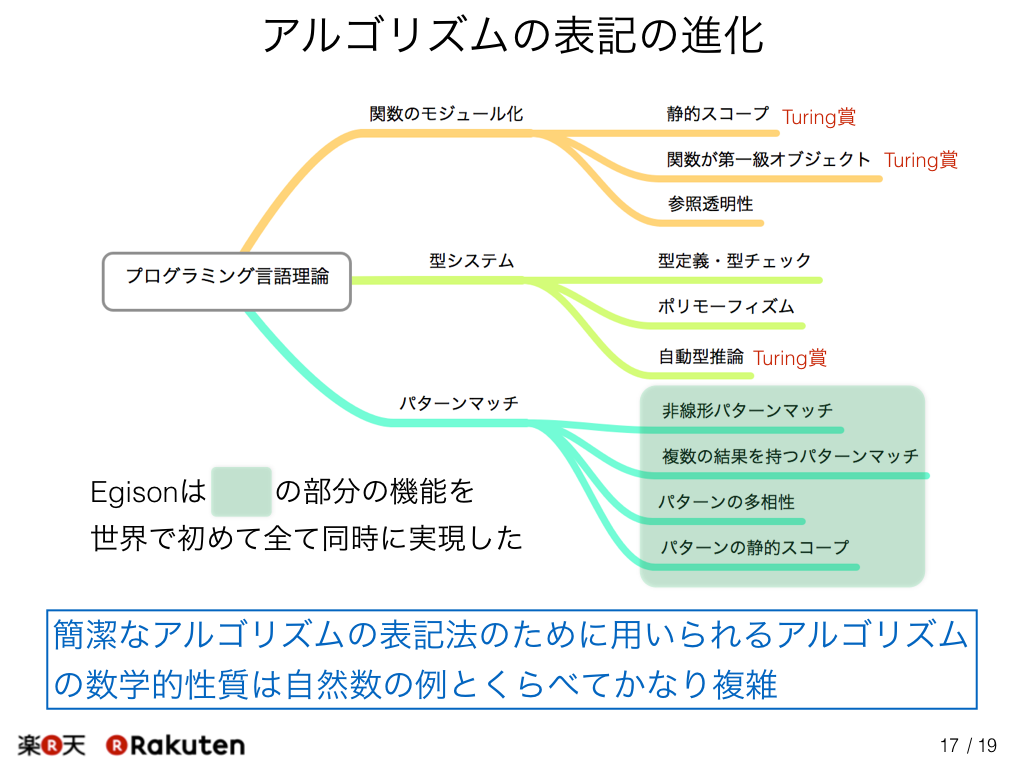
プログラミング言語の進化の歴史にも、数の表記の進化の歴史と似た流れをみることができます。 ただ、簡潔なアルゴリズムの表記法のために用いられるアルゴリズムの数学的性質は、 自然数の例とくらべて複雑でその理解は少し難しくなっています。

#18

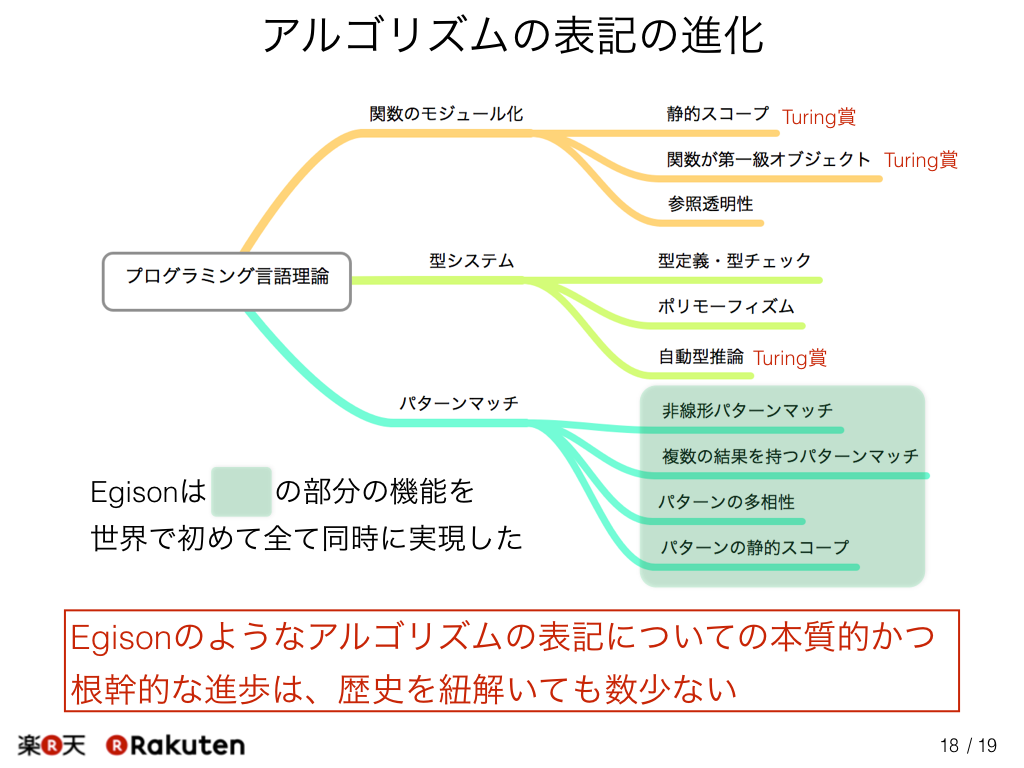
この図には現在のプログラミング言語の理論地図を書いています。 今までは表現の抽象化については、主に関数のモジュール化の理論と型システムの理論が深く研究されてきました。 その中でEgisonは、今まで他の理論に比べて貧弱であったパターンマッチの理論を大きく発展させることにより、既存の理論の大きな穴を埋めた研究であると私は考えています。 機会のあるときに試していただけたら幸いです。

#19

Egisonについていくつか文書を公開していますので読んでいただけたら嬉しいです。 またこれからも解説文など多く書く予定です。 Egisonの研究で生まれたアイデアが世の中に広まるのはまだまだ時間がかかりそうですが、今後とも応援していただければ幸いです。 ありがとうございました！