ゲーデルの不完全性定理の証明スケッチ

第一不完全性定理

数論を含む数学の理論を矛盾なく形式化すると、どのような公理系を用いて形式化しても、証明も反証もできない命題が存在する。

証明の概要

全ての論理式の集合は可算であり、自然数と一対一対応させることができる。
それゆえ、論理式は自然数でコード化できる。
エンコードのための関数をg(x)とする。
論理式をエンコードした数はゲーテル数と呼ばれる。

この関数の目的は、自己言及する命題を作成することにある。
例えば、「任意のF(x)について、

A ↔ F(g(A))                            - (1)

を満たすAが存在する」ことが証明できる。
この定理は対角化定理と呼ばれている。

有限の長さの論理式の列により、証明は表現できる。
それゆえ全ての証明の検証は有限時間で計算可能である。
そのため、

T ⊦ A → T ⊦ ∃ x.Proof(x, g(A))      - (2)

が成り立つ2変数関数Proof(x,y)を定義できる。
「T ⊦ A」とは、公理系Tのもとで命題Aは証明可能であるということを表す。
Proof(x, y)は自然数xに対応する証明が自然数yに対応する論理式の命題の証明であるということを表現する述語となる。
Provable(y) ⇔ ∃ x.Proof(x, y)と述語Provable(y)を定義すると(2)を以下のように書き換えることができる。

T ⊦ A → T ⊦ Provable(g(A))          - (2')

Provable(x)は自然数xが対応する命題の証明が存在するということを表現する述語となる。

Tがω-無矛盾という仮定を追加すると以下も成り立つ。

T ⊦ ∃ x.Proof(x, g(A)) → T ⊦ A      - (3)
T ⊦ Provable(g(A))     → T ⊦ A      - (3')

TODO: ω-無矛盾について説明追加

ここで、(1)のF(x)に¬Provable(x)を代入すると、

A ↔ ¬Provable(g(A))                - (4)

が得られる。
(4)の式を満たすようなAをGとおく。
このようなGはゲーテル文と呼ばれている。
Gを証明できると仮定すると、以下のように矛盾が生じる。

T ⊦ G ↔ T ⊦ Provable(g(G))           - (2'),(3')より
      ↔ T ⊦ ¬¬Provable(g(G))
      ↔ T ⊦ ¬G                       - (4)より

よってG,¬Gは両方とも公理系Tのもとでは証明できない。

対角化定理の証明の概要

「任意の1変数論理式F(x)について、

A ↔ F(g(A))     - (1)

を満たすAが存在する」ことを証明する。

全ての数項の集合は可算であり、列挙できる。
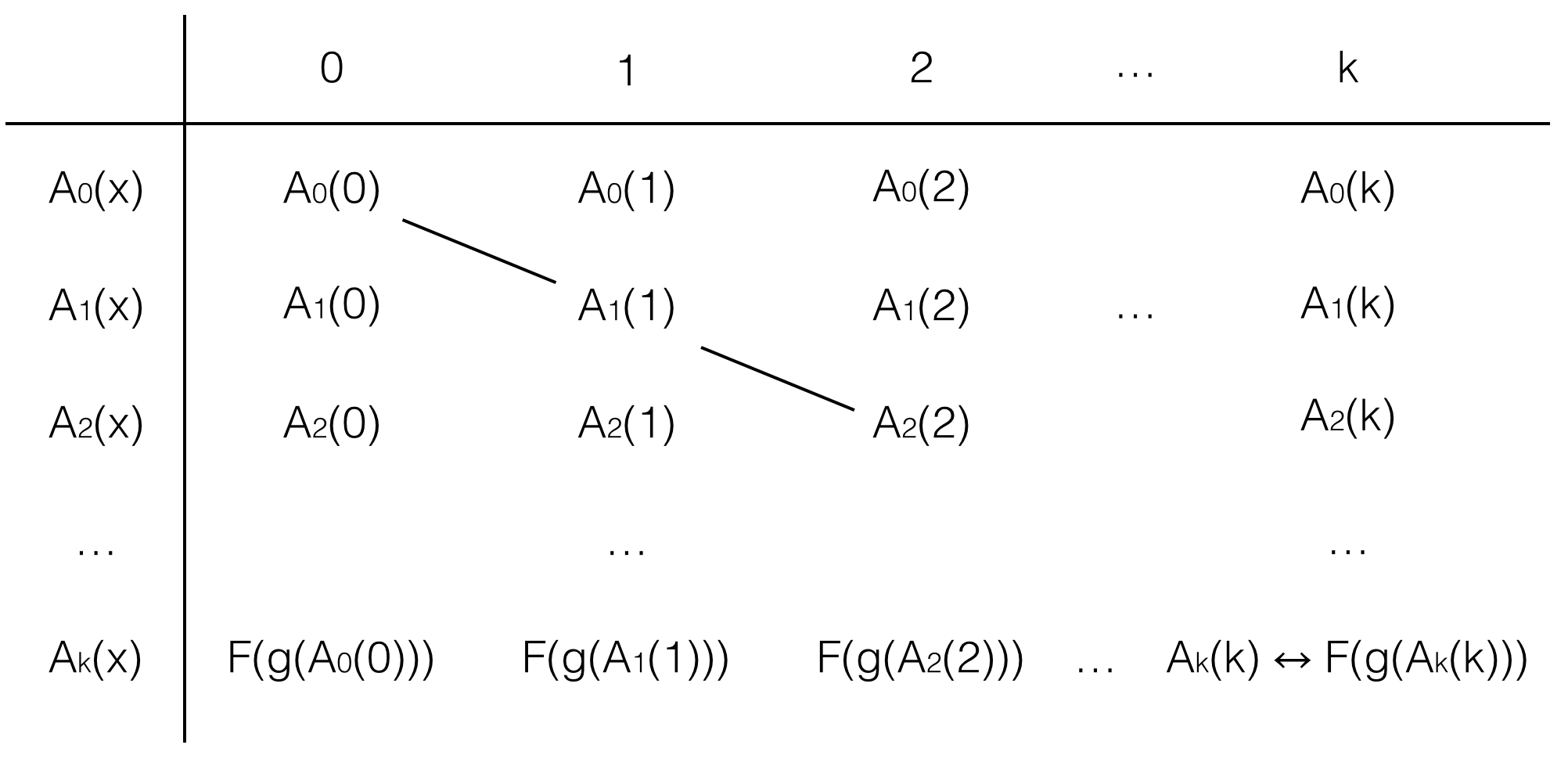
例えば、0,1,2,...という順番で列挙する。(図のテーブルの行見出し部分に対応する)

全ての1変数論理式の集合も可算であり、列挙できる。
例えば、g(x)を使ってエンコードした値が小さい順に並べる。
その列を、

A_0(x), A_1(x), A_2(x), ...     - (2)

とする。(図のテーブルの列見出し部分に対応する)

A_0(0), A_1(1), A_2(2), ...という命題の列を考える。(図のテーブルの対角線上に並ぶ列に対応する)
そして、

F(g(A_0(0)), F(g(A_1(1)), F(g(A_2(2)), ...

という命題の列を作り考える。(図のテーブルのA_k(x)の行の列に対応する)
B(x) = F(g(A_x(x))とおくと、このBは1変数論理式である。
そのため、B(x)は列(2)に含まれており、あるkについて

A_k(x) = B(x) = F(g(A_x(x))

である。
この式についてx = kを代入すると

A_k(k) = F(g(A_k(k))

が成り立っている。
このA_k(k)こそが、題意の命題Aである。

述語Proof(x, y)の計算可能性

厳密な証明のためには、述語Proof(x, y)の計算可能性についての議論が必要である。
このメモではその部分の証明については省略した。

[Top]